In a group of friends, each except one friend spies exactly one other friend. Every friend has some valuables, which is a positive integer. Find a group of friends with the biggest sum of valuables such that no friend spies any other friend within this group.

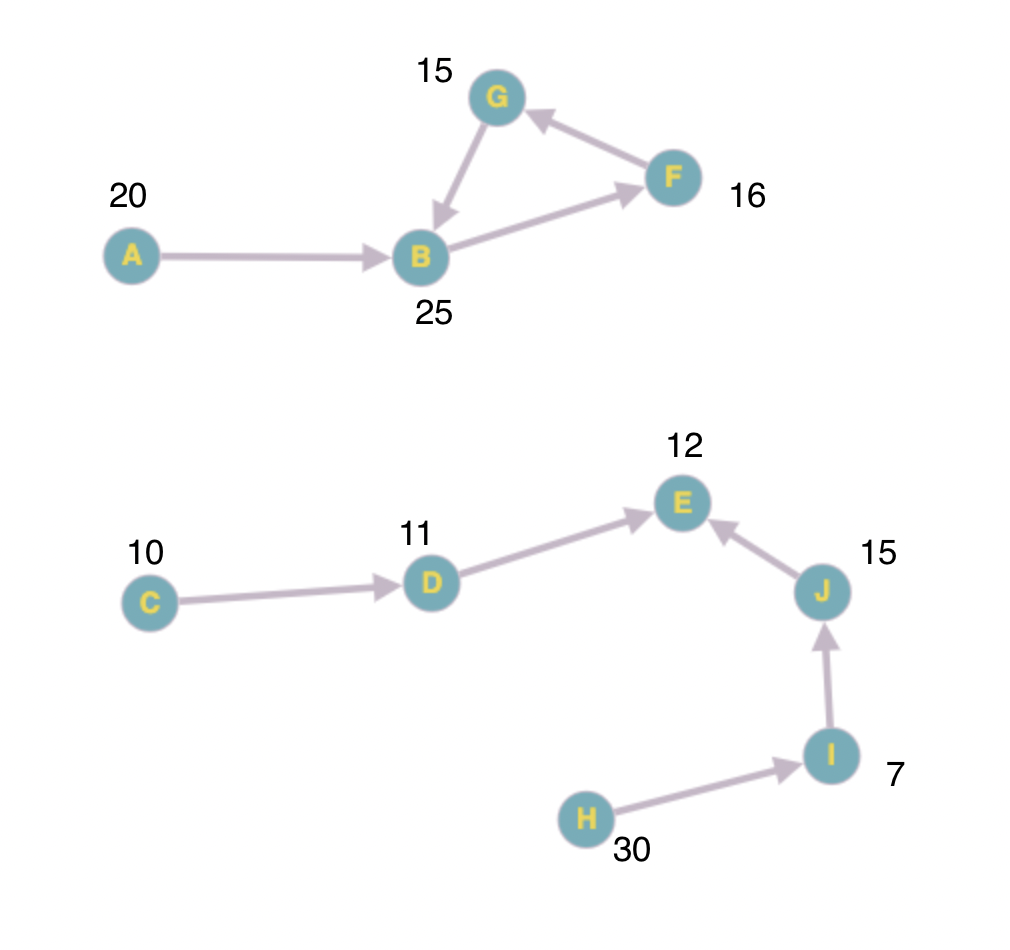
Example: We have the following graph for one of the possible test cases. The value above each vertex is the positive number of valuables owned by them.

The best possible group is [A,F,D,J,H] = 92 value

Looks like we can achieve the solution by ignoring the traversal through the graph and calculating the combinations of all possible groups. Unfortunately not able to think of a dynamic programming approach or how to get started.

CodePudding user response：

Give the constraints on your graph, you will always have:

• one disjoint connected sub-graph that is a tree consisting of zero-or-more simple paths all branching off the friend who is not spying on anyone; and
• zero-or-more disjoint connected sub-graphs where each sub-graph contains exactly one cycle and zero-or-more simple paths branching off the cycle.

To get the best sum of valuables:

• Within each branching path, there can be at most two non-selected vertices between each selected vertex. (If there were three non-selected vertices then you would get a better result if the middle vertex of those three were selected; i.e. (A)->B->C->D->(E) where () is a selected vertex will always give a better result as (A)->B->(C)->D->(E)).
• Within each cycle, unless blocked by a selected adjacent vertex in a branching path, there can be at most two non-selected vertices between each selected vertex. (for similar reasons to branching paths).

If you have the connected sub-graph (similar to the bottom of your example but E spies I, rather than spying nothing):

          -----------
          V         |
C -> D -> E -> I -> J <- H

Then you can either start with the cycle and work outwards to the branching paths or from the branching paths inwards. If you consider the cycle-outwards then:

• if E is selected then D, I and J cannot be and given that the minimum separation of 1 is achieved, then C and H must be selected.
• if I is selected then E and J cannot be selected and H and either C or D can be selected.
• if J is selected then E, I and H cannot be selected and either C or D can be selected.
• if none of the vertices on the cycle are selected then H and either C or D can be selected (which, in this case, is always a strictly worse option that selecting J as well, since it does not block selection from the branching paths).

This gives possible solutions for that connected sub-graph of:

• C, E, H
• C, I, H
• D, I, H
• C, J
• D, J

You can perform a similar operation for each disjoint subgraph and, for the one disjoint sub-graph containing the friend who is not spying on anyone then that friend can either be selected or not selected and each branching simple path can be evaluated independently choosing to either skip one-or-two vertices between selected vertices and finding the optimum total.

Find the solution with the highest value for the sub-graph and move on to the next sub-graph.