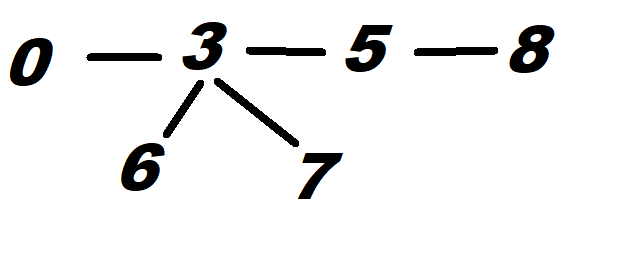We have an undirected acyclic graph where there is only a single path between two connected nodes that may look something like 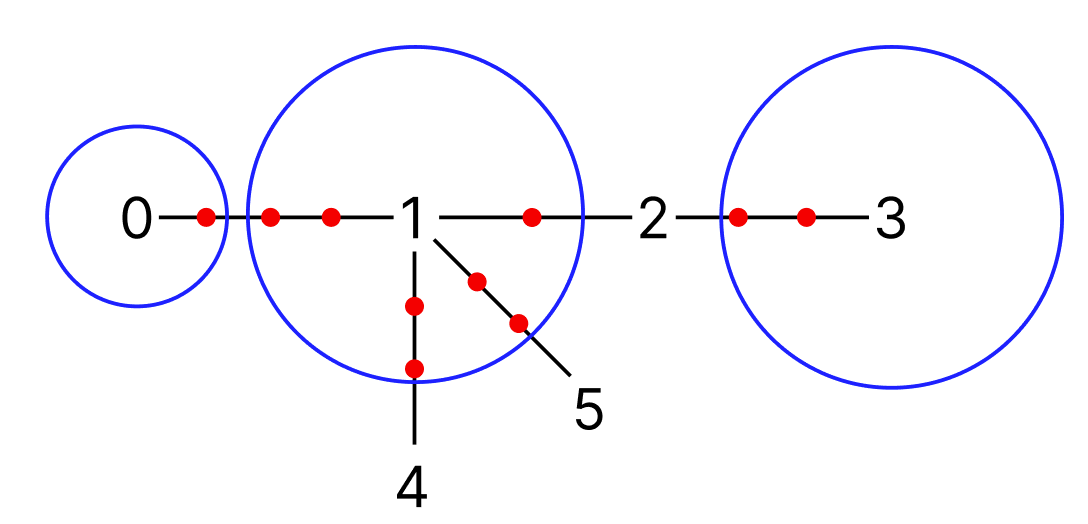 Simple guide to the image:
Simple guide to the image:
- Black numbers: Node id's (note that each node contains a resource collector)
- Resource collectors: Every resource collector collects resources on edges that are right next to it (so a collector on node 0 cannot reach resource deposits past node 1 and so on). A resource collector also requires fuel to operate - the amount of fuel a resource collector needs is directly connected to its range - the range determines the furthest resource node it can reach on the allowed edges (the range of the collectors is the blue circle on some nodes in the image). The fuel consumption of a collector is then calculated like this:
fuel = radius of the circle(meaning that in the example case node 0 consumes 1 fuel and node 1 and 3 consume 2 fuel each, and since all the resource deposits have been covered our final fuel requirement is 5 (nodes 2, 5 and 4 do not use any fuel, since their radii are 0)). - Black lines: Graph edges
- Red dots: Resource deposits, we only receive the number of deposits on a specific edge and all the deposits are evenly spaced apart on their respective edge.
Our task is to find the best configuration for our resource collectors (that is, find the configuration that consumes the lowest amount of fuel, and reaches all resource nodes) By this is meant: set the collector radius.
Things I've tried to solve this problem: At first I've tried locating the "central" node of the graph and then traversing it with BFS while checking one node ahead and determining the amount of fuel from there, this did work for some graphs, but it became unstable in more complex ones.
After that I've tried basically the same thing, but I chose the leaf nodes as the starting points, this produced similar, imperfect, results.
CodePudding user response:
This is an allocation problem.
- Set "cost" of each pair of collector and deposit it can reach to be the distance from collector to deposit. Other pairs, where the deposit is unreachable, have infinite cost and can be omitted from the input.
- Set collector/deposit pair with ( next ) lowest cost. Allocate deposit to collector. Repeat until all deposits allocated.
- Set radius of each collector to be the distance from the collector to the furthest deposit assigned to it.
Here is the cost of each pair in your example. 031 means the first deposit on the edge from 0 to 3
Note that you renumbered the nodes in your example!!! The numbers in the table refer to the original diagram which looked like this
| collector | deposit | cost |
|---|---|---|
| 0 | 031 | 1 |
| 0 | 032 | 2 |
| 0 | 033 | 3 |
| 3 | 031 | 3 |
| 3 | 032 | 2 |
| 3 | 033 | 1 |
| 3 | 351 | 1 |
| 3 | 361 | 1 |
| 3 | 362 | 2 |
| 3 | 371 | 1 |
| 3 | 372 | 2 |
| 5 | 351 | 1 |
| 5 | 581 | 1 |
| 5 | 582 | 2 |
| 6 | 361 | 2 |
| 6 | 362 | 1 |
| 7 | 371 | 2 |
| 7 | 372 | 1 |
| 8 | 581 | 2 |
| 8 | 582 | 1 |
Note that this algorithm will assign deposit 231 to collector 2. This is different from your answer, but has the same total fuel cost. However 142 will go to 4 and 152 will go to 5, which increases the total fuel cost.
To handle this situation, collectors with more than 2 connections to other nodes need to be looked at, to see if the fuel cost can be further reduced by increasing their radius, "robbing" deposits from their neighbors.
CodePudding user response:
This is not an allocation problem. There is a greedy optimal solution in O(n).
Here is the essence of the solution:
Let R(V,W) be the # of resource collectors on an edge between V & W. Note: R(V,W) == R(W,V) given the graph is undirected.
Set weight(V) = 0 for all vertices in the graph
1. A connected undirected acyclic graph is a forest.
2. Either the graph has 1 node (terminal case), or there is at least 1 vertex with degree 1. If the graph has 1 node, the algorithm is finished.
3. Select any vertex with degree 1. Let V be the vertex. Let W represent the other vertex connected to V.
4. weight(V) weight(W) >= # of resource collectors on the edge(V,W)
5. Since V has degree 1, it is strictly better to use fuel from node W.
6. Set weight(W) = max(weight(W), R(V,W) - weight(V)).
7. Remove V and E(V,W) from the graph. The resulting graph is still a connected undirected acyclic graph. Repeat until the graph is a single vertex.
Test case #1:
A - B - C - D - E. All edges have 1 resource collector
Select A. weight(B) = 1, since R(A,B) - weight(A) = 1.
Select B. weight(C) = 0, since R(B,C) - weight(B) = 0.
Select C. weight(D) = 1, since R(C,D) - weight(C) = 1.
Select D. weight(E) = 0, since R(D,E) - weight(D) = 0.
Test case #2:
A - B - C - D - E. R(A,B) = R(D,E) = 1. R(B,C) = R(C,D) = 2.
Select A. weight(B) = 1, since R(A,B) - weight(A) = 1.
Select E. weight(D) = 1, since R(D,E) - weight(E) = 1.
Select B. weight(C) = 1, since R(B,C) - weight(B) = 1.
Select C. weight(D) = 1, since max(weight(D), R(C,D) - weight(C)) = 1.