So I am doing a sample exam question in preparation for my stats exam and I have hit a dead end.
The question is asking:
If you roll two 6-sided fair dice until you get all possible outcomes (i.e. all sums 2-12 have occurred at least once). Estimate the expected number of dice rolls needed.
This question needs to be answered using a simulation study in R.
So far I have simulated two dice being rolled and have also obtained the sum of each roll. I am unsure how to modify my code to check for expected number of rolls needed to get each sum at least once
My code so far:
d <- data.frame(a=sample(1:6, 1000000, replace=TRUE),
b=sample(1:6, 1000000, replace=TRUE))
d$sum <- d$a d$b
hist(d$sum)
Any help would be great :))
CodePudding user response:
We can sample rolling a single die 10 times with the code:
sample(6, 10, TRUE)
If we want to sample two dice, we can use replicate on this code:
replicate(2, sample(6, 10, TRUE))
#> [,1] [,2]
#> [1,] 1 1
#> [2,] 4 5
#> [3,] 1 5
#> [4,] 2 2
#> [5,] 5 6
#> [6,] 3 6
#> [7,] 6 2
#> [8,] 2 1
#> [9,] 3 5
#> [10,] 3 5
So we can find the row sums of this matrix to get the sums from 10 rolls of 2 dice using rowSums:
rowSums(replicate(2, sample(6, 10, TRUE)))
#> [1] 2 9 6 4 11 9 8 3 8 8
Now supposing that we simulate 1,000 rolls of two dice in exactly the same way and call the output throws.
throws <- rowSums(replicate(2, sample(6, 1000, TRUE)))
It is almost certain we will have all of the values 2 - 12 in throws, but we can test it out:
length(unique(throws))
#> [1] 11
But we can also see that our first 11 throws were not enough to get all 11 different values:
length(unique(throws[1:11]))
#> [1] 10
What if we look at the first 100 throws?
length(unique(throws[1:100]))
#> [1] 11
So we know that somewhere between 11 and 100 throws were required. Now if we iterate through these throws, then we will find the first point where the number of unique throws was 11:
for(i in 11:100)
{
if(length(unique(throws[1:i])) == 11) break;
}
i
#> [1] 23
Our loop stopped when i was 23, meaning that it took 23 throws to get all 11 unique sums from our two dice.
We can wrap all this logic in a little function:
sim <- function() {
throws <- rowSums(replicate(2, sample(6, 1000, TRUE)))
for(i in 11:1000)
{
if(length(unique(throws[1:i])) == 11) break;
}
return(i)
}
And we will see we get a different number each time:
sim()
#> [1] 29
sim()
#> [1] 94
sim()
#> [1] 62
If we want a feel for the distribution of results of sim, we need to put a bunch of its results in a vector. Again, we can use replicate here:
vec <- replicate(1000, sim())
Now we can see the mean number of throws required:
mean(vec)
#> [1] 59.821
And the median
median(vec)
#> [1] 51
And a histogram:
hist(vec)
Or a density plot:
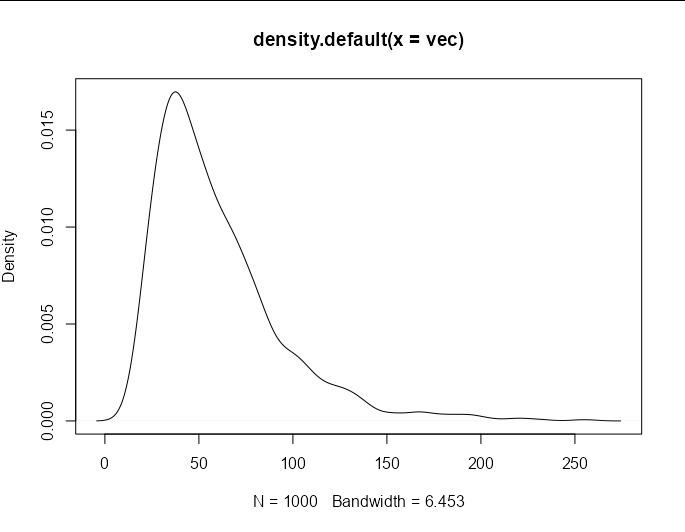
plot(density(vec))
CodePudding user response:
I had looked at this problem and as it is exam related thought a through explanation was not appropriate. That was my read of:
How do I ask and answer homework questions?
I am new to this forum. What do others think?
This was the hint that I provided, which was downvoted.
I don't want to do the problem for you, but after simulating a million rolls you want go through them and find the first time that you have seen at least one roll of each possible outcome (2,3,...,12) and record that time.