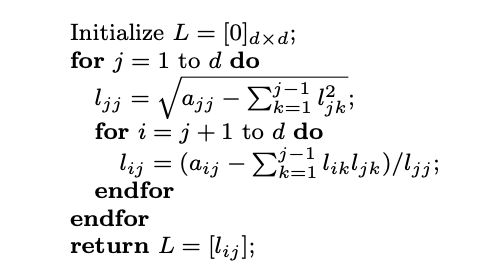Cholesky factorisation not lower triangular-CodePudding

I am building a cholesky factorisation algorthim as proposed from the book:

Linear Algebra and Optimisation for Machine Learning

They provide the following algorthim:

I have attempted this with python with the following algorithm:

def CF(array):
    array = np.array(array, float)
    arr = np.linalg.eigvals(array)
    for o in arr:
        if o < 0:
            return print('Cannot apply Cholesky Factorisation')
        else:
            continue
            
    L = np.zeros_like(array)
    n,_ = array.shape
    for j in range(n):
        sumkj = 0
        for k in range(j):
            sumkj  = L[j,k]**2
            print(array[j,j], sumkj)
        L[j,j] = np.sqrt(array[j,j] - sumkj)
        for i in range(j 1):
            sumki = 0
            for ki in range(i):
                sumki  = L[i,ki]
            L[i,j] = (array[i,j] - sumki*sumkj)/L[j,j]
    return L

When testing this on a matrix I get upper triangular as opposed to lower triangular. Where was I mistaken?

a = np.array([[4, 2, 1], [2, 6, 1], [2, 8, 2]])

CF(a)
>array([[2.        , 0.81649658, 0.70710678],
       [0.        , 2.44948974, 0.70710678],
       [0.        , 0.        , 1.41421356]])

CodePudding user response：

You don't even need to look at the detail of the algorithm.

Just see that in your book algorithm you have

for j=1 to d
    L(j,j) = something
    for i=j 1 to d
        L(i,j) = something

So, necessarily, all elements whose line number i is greater or equal than column number j are filled. Rest is 0. Hence a lower triangle

In your algorithm on another hand you have

for j in range(n):
    L[j,j] = something()
    for i in range(j 1):
        L[i,j] = something()

So all elements whose line number i is < to column number j, 1 (since i is in range(j 1), that is i<j 1, that is i<=j) are filled with something. Rest is 0.

Hence upper triangle

You probably wanted to

    for i in range(j 1, n)