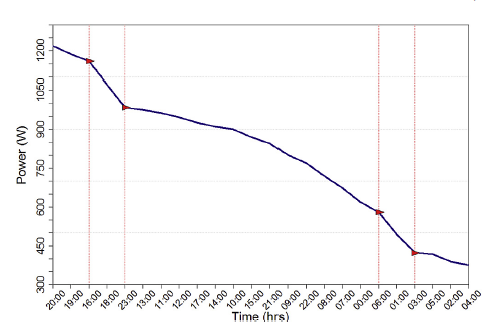
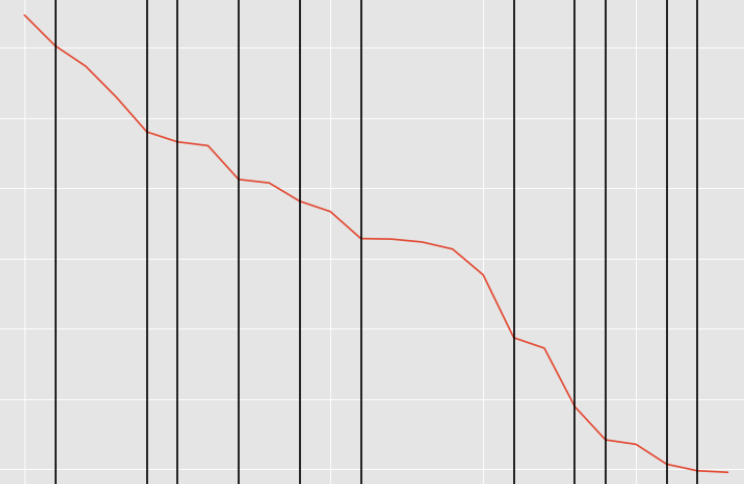
I want to come up with a plot that shows the inflection points of a curve as follows:
I have a somewhat similar curve and I want to compute somehow the inflection points by using python. My curve looks as follows:
I am using the following code to compute the inflection points:
def find_inflection_points(df, n=1):
raw = df['consumption'].to_numpy()
infls = []
dx = 0
for i, x in enumerate(np.diff(raw, n)):
if x >= dx and i > 0:
infls.append(i*n)
dx = x
# plot results
plt.plot(raw, label='Input Data')
for i, infl in enumerate(infls, 1):
plt.axvline(x=infl, color='k', label=f'Inflection Point {i}')
plt.legend(bbox_to_anchor=(1.55, 1.0))
return infls
However, I am getting the following plot:
I would expect less inflection points. Any idea of what should I change or any other proposal for implementation?
EDIT:
The data is the following:
raw = np.array([52.33,
50.154444444444444,
48.69222222222223,
46.49111111111111,
44.01444444444444,
43.30555555555556,
43.034444444444446,
40.62888888888889,
40.38111111111111,
39.07666666666667,
38.339999999999996,
36.41444444444445,
36.37888888888889,
36.17111111111111,
35.666666666666664,
33.827777777777776,
29.35222222222222,
28.60888888888889,
24.43,
22.078888888888887,
21.756666666666664,
20.345555555555556,
19.874444444444446,
19.763333333333335])
CodePudding user response:
So, strictly speaking, inflection point is indeed a change of sign of curvature. Which, for a 3 times differenciable function, is a point at which there is a change of sign of the 2nd derivative (the second derivative is 0, and the third derivative is not).
In your case, since the data are very discrete (only 24 data, one per hour in the day, I surmise), it is quite tricky to talk about second and third derivative. But if we give a try, we can see that, not only the point you are interested in are not inflection points (when the second derivative is 0, that means that the first derivative is locally constant. Which means that the slope is constant. And the points you seem to be interested in are, on the contrary, points where there is a change of slope. The the opposite of an inflection point!.
They are tho, inflection points of the derivative, since it seems that they are local extremum of the second derivative, so, at least if we had a continuous enough curve to dare speak of 3rd derivative, one could that that the extrema of second derivative are the 0 of the 3rd derivative. And 3rd derivative is the 2nd derivative of the 1st derivative. So, you could say that you are interested in the inflection points of the 1st derivative, that is of the slope.
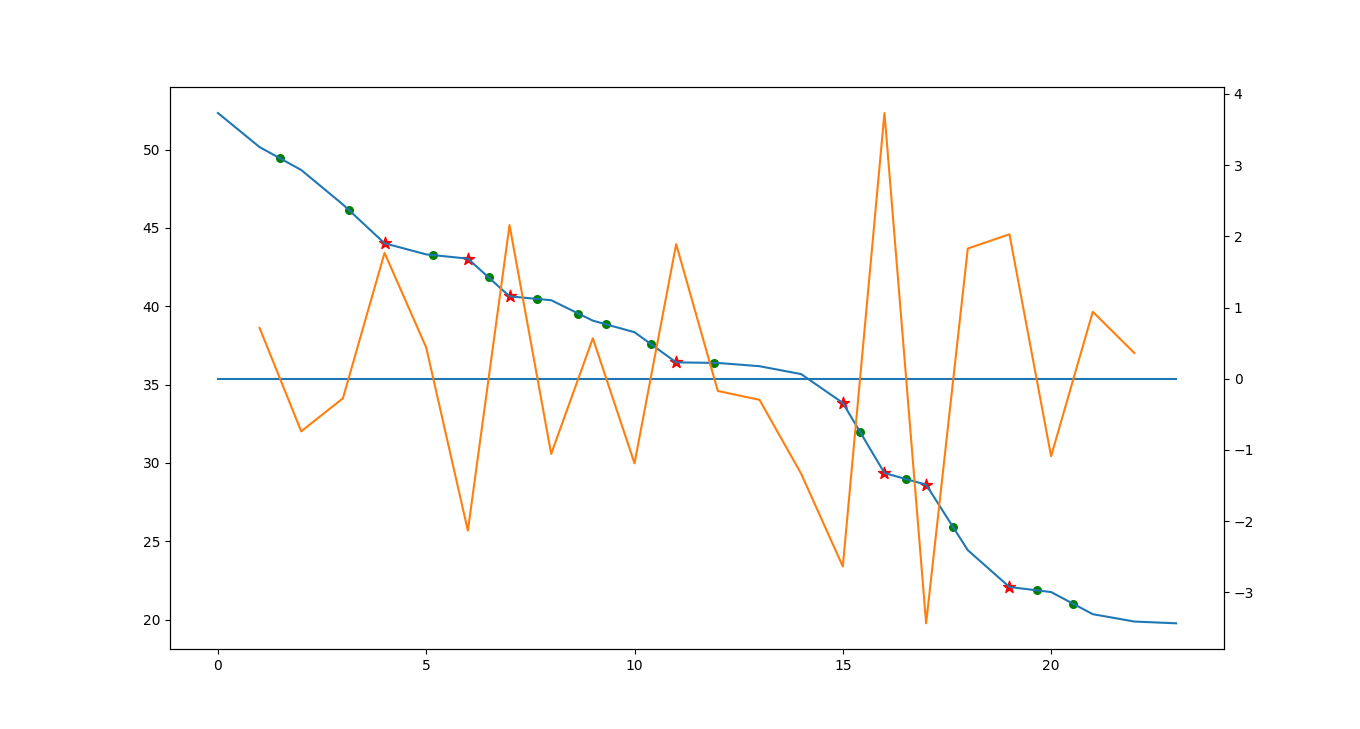
See code below:
import numpy as np
from matplotlib import pyplot as plt
raw = np.array([52.33, 50.154444444444444, 48.69222222222223, 46.49111111111111, 44.01444444444444, 43.30555555555556, 43.034444444444446, 40.62888888888889, 40.38111111111111, 39.07666666666667, 38.339999999999996, 36.41444444444445, 36.37888888888889, 36.17111111111111, 35.666666666666664, 33.827777777777776, 29.35222222222222, 28.60888888888889, 24.43, 22.078888888888887, 21.756666666666664, 20.345555555555556, 19.874444444444446, 19.763333333333335])
x=np.arange(24)
rawb=np.roll(raw, 1)
rawa=np.roll(raw,-1)
der2=rawb rawa-2*raw
der2[0]=der2[-1]=np.nan
der2abs=np.abs(der2)
offs = der2abs/(der2abs np.roll(der2abs, -1))
yoffs = raw*(1-offs) rawa*offs
chsign=(der2*np.roll(der2,-1))<0
s=1.5
mxder2 = (((der2>np.roll(der2,-1)) & (der2>np.roll(der2,1))) | ((der2<np.roll(der2,-1)) & (der2<np.roll(der2,1)))) & (der2abs>s)
fig, ax=plt.subplots()
ax2=ax.twinx()
ax.plot(raw)
ax2.plot([0]*24)
ax2.plot(der2)
ax.scatter(x[mxder2], raw[mxder2], 80, c='r', marker='*')
ax.scatter((x offs)[chsign], yoffs[chsign], 30, c='g', marker='o')
plt.show()
The blue line are your data.
The orange line is the second derivative.
The green dots are the points where second derivative is 0.
While the red stars are the points where second derivative is an extrema (with a minimum absolute value: we don't count local extrema of area where second derivative is almost flatlining 0).
From what you have shown, you seem more interested in red stars! The green dots are not just too numerous. Even filtering them (from an unknown criteria) would not do: they are all quite boring!
What makes the situation, and the vocabulary, ambiguous is the fact that we are talking about discrete points in reality. Inflection point are points where second derivative is 0. That is where 1st derivative is an extrema. And you need on the contrary points where second derivative is extreme. On so discrete set of data, you can be both tho. And maybe that was the case in your paper: points with sharp change of slopes are points where second derivative are extremely positive, but is surronded by 2 extremely negative second derivative (or the opposite).
But, my point is, you seem more interested in red stars.
As for how I compute that:
der2 is the second derivative, using discrete scheme y[-dt]-2y[0] y[dt]
der2abs is its absolute value.
offs is a barycenter weighted by successive values of der2abs. Where there is a change of sign of the 2nd derivative, between index i and i 1, this account for an estimation of the exact position of the 0: offs is 0 if the 0 is at index i, 1 if it is at index 1, 0.5 if it is in the middle between i and i 1, etc. offs makes no sense where there is no change of sign (and we won't use those values).
yoffs is the raw value using the same barycenter. So, yoffs is yoffs[i], yoffs[i 1], yoffs[i 0.5] in the 3 previous cases (what would be yoffs[i 0.5] were a legal thing). Like offs, makes sense only where there is a change of sign of der2.
chsign is precisely what says where those change of sign occur.
So, we just have to plot yoffs[chsign] vs (x offs)[chsign] to filter the cases where the second derivative are 0.
The red stars are easier to compute: We just find all the points whose second derivative is either bigger or smaller than its 2 neighbor. And filter those to add a minimum value condition (|secondDerivative| must be at least 1.5)