We are trying to fit a binomial model to our proportion data in a microbiology experiment where we counted the number of resistant and susceptible colonies exposed to different durgs (plate in the data frame). These are done on plates using a small amount of culture (20µl), and then (normally) scaled up to cells per mL. This can obviously give very high numbers of total cells (in the billions at times).
We fitted a generalised linear mixed effects model using glmer() and it was very overdispersed. Then we tried using cells per µl (1000-fold lower), and the model gave the same predictions, but also a much lower value for overdispersion.
Am just wondering why this happens (although I am pretty certain it is due to the high counts), and also what anyone would recommend for these sorts of analyses going forwards in terms of what scale/unit to do the analyses.
# does it matter what plate counts are corrected to for a glmer?
# Load packages ####
library(lme4)
#> Loading required package: Matrix
library(blmeco)
#> Loading required package: MASS
library(tidyverse)
# read in example
d_example <- tibble::tribble(
~treatment, ~plate, ~count_cor_ul, ~count_susc_ul, ~total_count_ul, ~prop_ul, ~count_cor_ml, ~count_susc_ml, ~total_count_ml, ~prop_ml,
"0_1", "amp", 3600, 8900, 12500, 0.288, 3600000, 8900000, 12500000, 0.288,
"0_1", "azi", 750, 11750, 12500, 0.06, 750000, 11750000, 12500000, 0.06,
"0_1", "cef", 5, 12495, 12500, 4e-04, 5000, 12495000, 12500000, 4e-04,
"0_1", "cip", 150, 12350, 12500, 0.012, 150000, 12350000, 12500000, 0.012,
"0_1", "gen", 5450, 7050, 12500, 0.436, 5450000, 7050000, 12500000, 0.436,
"0_1", "tet", 285, 12215, 12500, 0.0228, 285000, 12215000, 12500000, 0.0228,
"0_2", "amp", 650, 11500, 12150, 0.0534979423868313, 650000, 11500000, 12150000, 0.0534979423868313,
"0_2", "azi", 210, 11940, 12150, 0.0172839506172839, 210000, 11940000, 12150000, 0.0172839506172839,
"0_2", "cef", 40, 12110, 12150, 0.00329218106995885, 40000, 12110000, 12150000, 0.00329218106995885,
"0_2", "cip", 150, 12000, 12150, 0.0123456790123457, 150000, 1.2e 07, 12150000, 0.0123456790123457,
"0_2", "gen", 7900, 4250, 12150, 0.650205761316872, 7900000, 4250000, 12150000, 0.650205761316872,
"0_2", "tet", 110, 12040, 12150, 0.00905349794238683, 110000, 12040000, 12150000, 0.00905349794238683,
"0_3", "amp", 3400, 24100, 27500, 0.123636363636364, 3400000, 24100000, 27500000, 0.123636363636364,
"0_3", "azi", 1750, 25750, 27500, 0.0636363636363636, 1750000, 25750000, 27500000, 0.0636363636363636,
"0_3", "cef", 115, 27385, 27500, 0.00418181818181818, 115000, 27385000, 27500000, 0.00418181818181818,
"0_3", "cip", 455, 27045, 27500, 0.0165454545454545, 455000, 27045000, 27500000, 0.0165454545454545,
"0_3", "gen", 12800, 14700, 27500, 0.465454545454545, 12800000, 14700000, 27500000, 0.465454545454545,
"0_3", "tet", 4000, 23500, 27500, 0.145454545454545, 4e 06, 23500000, 27500000, 0.145454545454545,
"0_4", "amp", 3900, 2700, 6600, 0.590909090909091, 3900000, 2700000, 6600000, 0.590909090909091,
"0_4", "azi", 50, 6550, 6600, 0.00757575757575758, 50000, 6550000, 6600000, 0.00757575757575758,
"0_4", "cef", 10, 6590, 6600, 0.00151515151515152, 10000, 6590000, 6600000, 0.00151515151515152,
"0_4", "cip", 50, 6550, 6600, 0.00757575757575758, 50000, 6550000, 6600000, 0.00757575757575758,
"0_4", "gen", 4500, 2100, 6600, 0.681818181818182, 4500000, 2100000, 6600000, 0.681818181818182,
"0_4", "tet", 300, 6300, 6600, 0.0454545454545455, 3e 05, 6300000, 6600000, 0.0454545454545455,
"0_5", "amp", 850, 7150, 8000, 0.10625, 850000, 7150000, 8e 06, 0.10625,
"0_5", "azi", 350, 7650, 8000, 0.04375, 350000, 7650000, 8e 06, 0.04375,
"0_5", "cef", 80, 7920, 8000, 0.01, 80000, 7920000, 8e 06, 0.01,
"0_5", "cip", 220, 7780, 8000, 0.0275, 220000, 7780000, 8e 06, 0.0275,
"0_5", "gen", 4200, 3800, 8000, 0.525, 4200000, 3800000, 8e 06, 0.525,
"0_5", "tet", 640, 7360, 8000, 0.08, 640000, 7360000, 8e 06, 0.08
)
# ok want to fit a binomial model to see if resistance changes between drugs and antibiotics
# try and fit model to the ml data
mod1 <- glmer(cbind(count_cor_ml, count_susc_ml) ~ plate (1|treatment), d_example, family = binomial)
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, : Model is nearly unidentifiable: very large eigenvalue
#> - Rescale variables?
# check for overdispersion (it should not be over 1.4)
blmeco::dispersion_glmer(mod1)
#> [1] 656.0779
# fit using microlitre data
mod2 <- glmer(cbind(count_cor_ul, count_susc_ul) ~ plate (1|treatment), d_example, family = binomial)
# check for overdispersion (it should not be over 1.4)
blmeco::dispersion_glmer(mod2)
#> [1] 20.75102
# do the predictions of the model change?
# we can plot the model predictions easy enough
preds1 <- emmeans::emmeans(mod1, ~plate, type = 'response') %>%
data.frame() %>%
janitor::clean_names() %>%
mutate(pred = 'ml')
preds2 <- emmeans::emmeans(mod2, ~plate, type = 'response') %>%
data.frame() %>%
janitor::clean_names() %>%
mutate(pred = 'ul')
preds <- bind_rows(preds1, preds2) %>%
left_join(., dplyr::select(d_example, plate) %>% distinct())
#> Joining, by = "plate"
# plot data
ggplot(d_example)
geom_line(aes(plate, prop_ul, group = treatment), col = 'light grey')
geom_point(aes(plate, prob, col = pred), preds, position = position_dodge(0.7), size = 3)
geom_linerange(aes(ymin = asymp_lcl, ymax = asymp_ucl, x = plate, col = pred), position = position_dodge(0.7), preds)
geom_point(aes(plate, prop_ul), shape = 21, fill = 'white')
theme_bw()
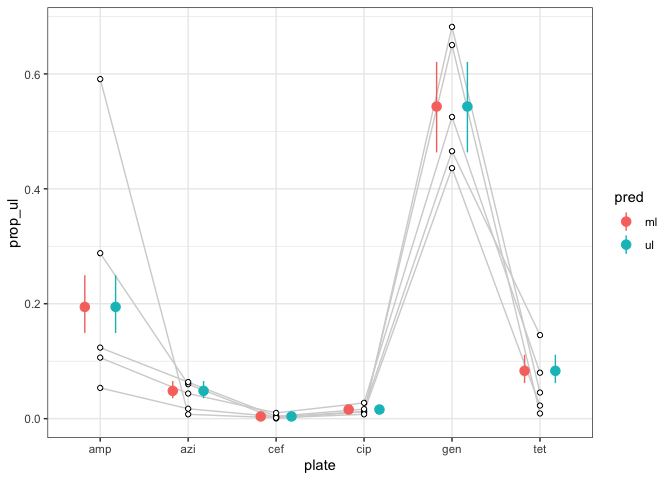
Created on 2022-12-12 with reprex v2.0.2
PS. in reality we ended up fitting a beta binomial in brms which fit the data great.
CodePudding user response:
dispersion_glmer calculates "the square root of the penalized residual sum of squares divided by n". The result is not unit-less.
20.75102 * sqrt(1000)
#[1] 656.2049
(Machine precision and convergence issues could also play a limited role here.)
CodePudding user response:
This is really a statistical question. You shouldn't be using a binomial model on data that aren't raw counts (there may be some rare exceptions ...)
At a quick glance, it looks like a square-root-transformed linear mixed model would probably be fine for this.
gg0 <- ggplot(d_example, aes(plate, prop_ul)) geom_point()
geom_line(aes(group=treatment))
gg0 scale_y_sqrt()
gg0 scale_y_log10()
You could also fit a Beta model (in brms or glmmTMB) or a quasi-binomial model (glmer doesn't do quasi-binomial but there is code in the GLMM FAQ which shows how to compute the quasi-likelihood standard errors/p-values), if you think the denominators are likely to affect the variances.
It is also the case that a binomial model without some kind of overdispersion correction is likely to be ridiculously optimistic when the counts are large.
