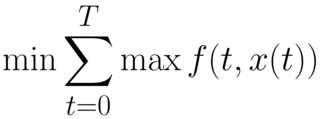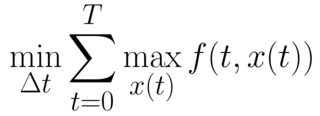Can GEKKO solve Minimax Optimal Control problems?-CodePudding

I'm aware that GEKKO can solve minimax optimization problems as well as optimal control problems. However, is there a mechanism on GEKKO to solve a minimax/maximin optimal control problem such as:

More specifically,

CodePudding user response：

There is no issue to combine minimax with optimal control. There is also information on minimizing final time with the

import numpy as np
from gekko import GEKKO
import matplotlib.pyplot as plt

m = GEKKO()
nt = 501; tm = np.linspace(0,1,nt); m.time = tm

# Variables
x1 = m.Var(value=np.pi/2.0)
x2 = m.Var(value=4.0)
x3 = m.Var(value=0.0)

p = np.zeros(nt)
p[-1] = 1.0
final = m.Param(value=p)

# FV
tf = m.FV(value=1.0,lb=0.1,ub=100.0)
tf.STATUS = 1

# MV
u = m.MV(value=0,lb=-2,ub=2)
u.STATUS = 1

m.Equation(x1.dt()==u*tf)
m.Equation(x2.dt()==m.cos(x1)*tf)
m.Equation(x3.dt()==m.sin(x1)*tf)

m.Equation(x2*final<=0)
m.Equation(x3*final<=0)

m.Minimize(tf)

m.options.IMODE = 6
m.solve()

print('Final Time: '   str(tf.value[0]))

tm = tm * tf.value[0]

plt.figure(1)
plt.plot(tm,x1.value,'k-',lw=2,label=r'$x_1$')
plt.plot(tm,x2.value,'b-',lw=2,label=r'$x_2$')
plt.plot(tm,x3.value,'g--',lw=2,label=r'$x_3$')
plt.plot(tm,u.value,'r--',lw=2,label=r'$u$')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()

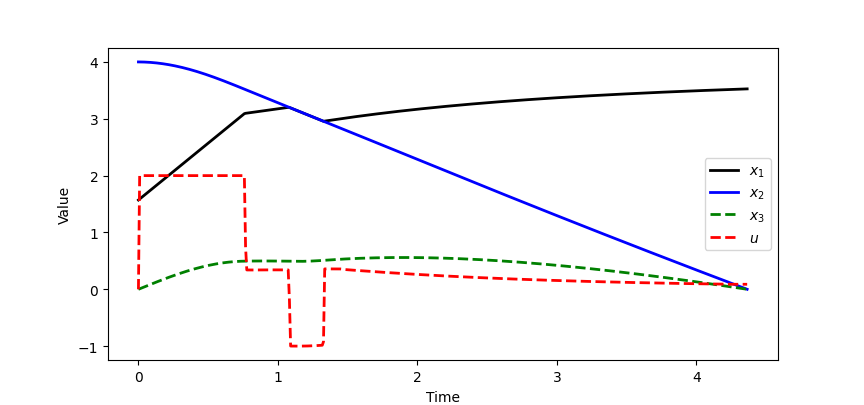
Combining these two types of problems:

import numpy as np
from gekko import GEKKO
import matplotlib.pyplot as plt

m = GEKKO()

nt = 501
tm = np.linspace(0,1,nt)
m.time = tm

x1 = m.Var(value=np.pi/2.0)
x2 = m.Var(value=4.0)
x3 = m.Var(value=0.0)

p = np.zeros(nt)
p[-1] = 1.0
final = m.Param(value=p)
tf = m.FV(value=1.0,lb=0.1,ub=100.0)
tf.STATUS = 1
m.Minimize(tf)

Z = m.Var()
m.Minimize(Z)
m.Equations([Z>=x1,Z>=x2,Z>=x3])
m.Maximize(x1)
m.Maximize(x2)
m.Maximize(x3)

u = m.MV(value=0,lb=-2,ub=2)
u.STATUS = 1

m.Equation(x1.dt()==u*tf)
m.Equation(x2.dt()==m.cos(x1)*tf)
m.Equation(x3.dt()==m.sin(x1)*tf)

m.Equation(x2*final<=0)
m.Equation(x3*final<=0)

m.options.IMODE = 6
m.solve()

print('Final Time: '   str(tf.value[0]))

tm = tm * tf.value[0]

plt.figure(1)
plt.plot(tm,x1.value,'k-',lw=2,label=r'$x_1$')
plt.plot(tm,x2.value,'b-',lw=2,label=r'$x_2$')
plt.plot(tm,x3.value,'g--',lw=2,label=r'$x_3$')
plt.plot(tm,u.value,'r--',lw=2,label=r'$u$')
plt.legend(loc='best')
plt.xlabel('Time')
plt.ylabel('Value')
plt.show()