Convolution of a Gaussian with an asymmetrical Gaussian-CodePudding

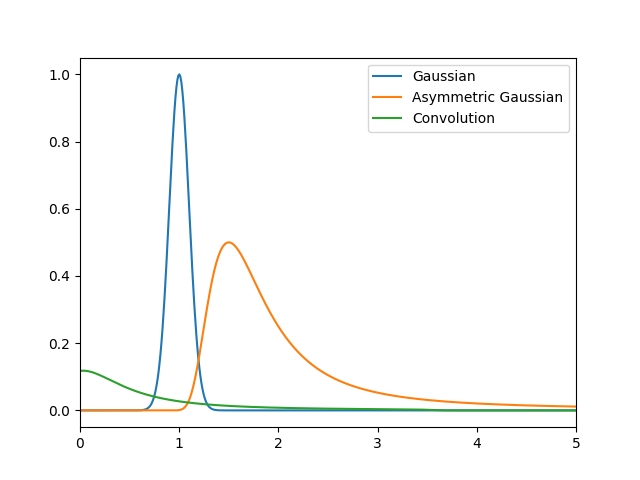
I'm looking to convolve a Gaussian with an asymmetric Gaussian. My attempt at this is below.

import numpy as np
import matplotlib.pyplot as plt

x=np.linspace(0,5,500)
dx=x[1]-x[0]

# Gaussian
sigma1=0.1
peak1=1
gauss1=np.exp(-(x-peak1)**2/(2*sigma1**2))

# Asymmetric Gaussian
gauss2=0.5*np.exp(-(x-1.5)**2/(-0.2 x*0.4)**2)

# convolution
conv=np.convolve(gauss1,gauss2,mode='same')*dx

plt.plot(x,gauss1,label='Gaussian')
plt.plot(x,gauss2,label='Asymmetric Gaussian')
plt.plot(x,conv,label='Convolution')
plt.xlim(0,5)
plt.legend()
plt.show()

I don't understand why the resultant curve is positioned where it is. I would have thought it would have a peak at some x location between that of the two original curves?

CodePudding user response：

Let me try to describe the math part

In the convolution of two functions, the resulting curves peak is determined by the relative positions and shapes of the two original functions.

As the wider function will contribute more to the convolution at positions further away from its peak, resulting in a peak closer to its position.

So the position of the peak in the convolution can be adjusted by changing the position of one of the original functions. The peak of the convolution is the point at which the curve reaches its maximum value.

CodePudding user response：

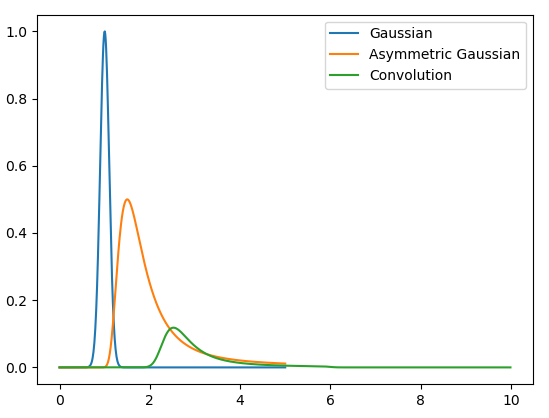
The problem is that in the convolution function, you used the parameter mode='same'. This mode only returns the middle values of the convolution as described in the official documentation. To get the actual convolution output, you need to use mode='full' to get the entire convolution result. In your case, given two inputs of 500 values, the output will have a size of 500 500 - 1 = 999.

Here's the edited code.

import numpy as np
import matplotlib.pyplot as plt

x=np.linspace(0,5,500)
dx=x[1]-x[0]

# Gaussian
sigma1=0.1
peak1=1
gauss1=np.exp(-(x-peak1)**2/(2*sigma1**2))

# Asymmetric Gaussian
gauss2=0.5*np.exp(-(x-1.5)**2/(-0.2 x*0.4)**2)

# convolution
x1 = np.linspace(0,9.99,999)
conv=np.convolve(gauss1,gauss2,mode='full')*dx

plt.plot(x,gauss1,label='Gaussian')
plt.plot(x,gauss2,label='Asymmetric Gaussian')
plt.plot(x1, conv,label='Convolution')
plt.legend()
plt.show()

The resultant peak need not lie in between that of the original curves. Say your peak was at 1 and 1.5. The resultant peak will be at 1 1.5 = 2.5.