Plotting lemniscates on a polar curve doesn't show the point at r = 0-CodePudding

import numpy as np
import matplotlib.pyplot as plt

a = 2 
rads = np.arange(0, 360, 0.001)
r_vals = []

for rad in rads:
    r = a*(np.sqrt(np.sin(2*rad)))
    r_vals.append(r)

fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})
ax.plot(rads, r_vals)

ax.set_rlabel_position(22)
ax.grid(True)

ax.set_title("A line plot on a polar axis", va='bottom')
plt.show()

this code gives this as the output:

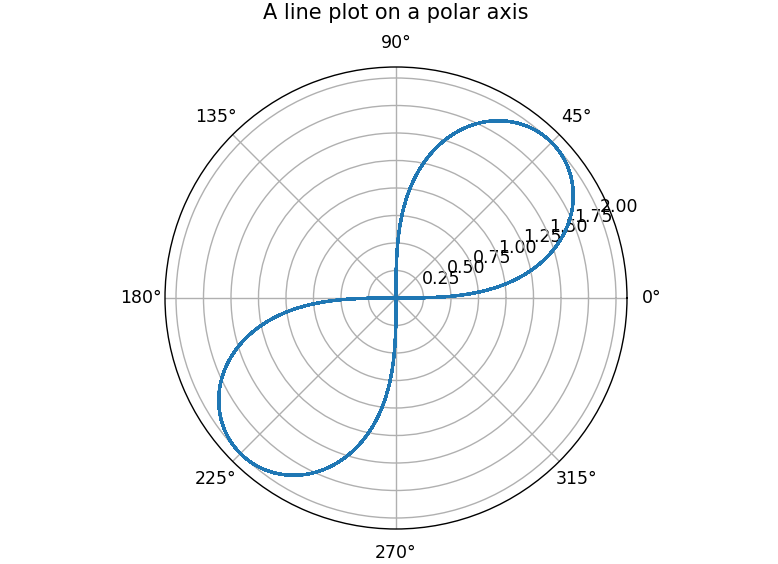
which looks good until you zoom in,

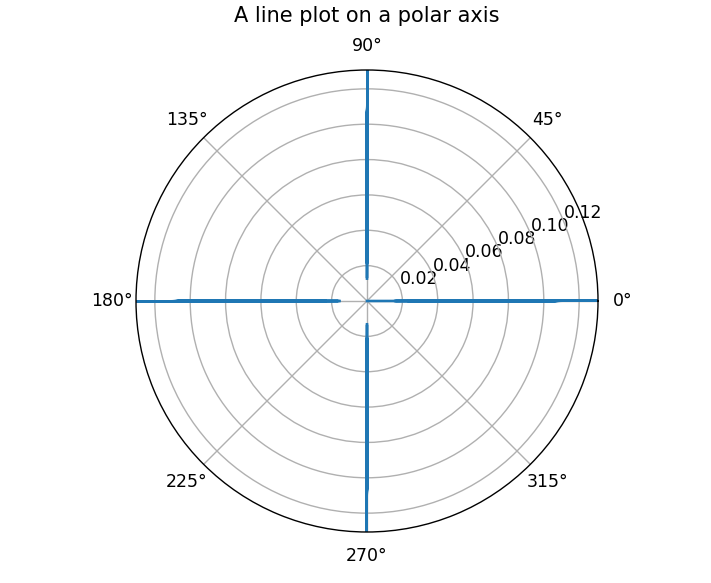
is there anyway where i could connect the lines?

CodePudding user response：

Plotting this using the direct polar form is not a good choice, in particular since the resolution of the curve will change dramatically close to the asymptotes and half of the angular domain is out of the defined bounds of the function.

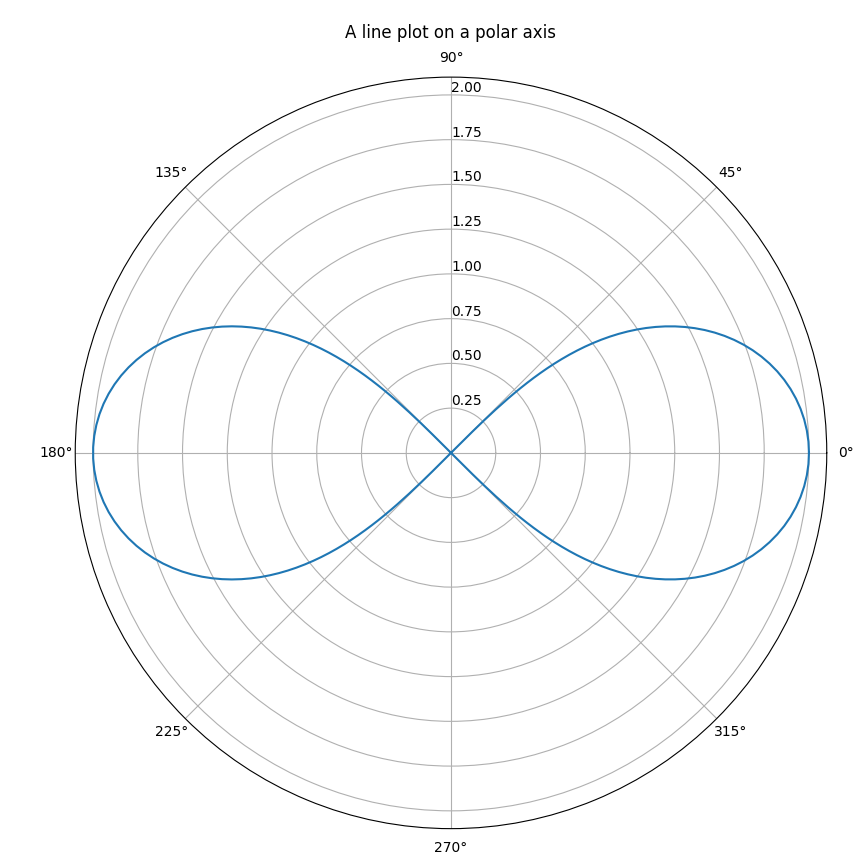
To ensure a continuous resolution of the curve and to guarantee selection of a valid angular domain, use the parametric form. I show this in the canonical orientation (i.e., with the lobes along the x-axis); if you really need that to change then add a phase shift.

import numpy as np
import matplotlib.pyplot as plt

'''
https://en.wikipedia.org/wiki/Lemniscate_of_Bernoulli
Original solution was in the form of polar coordinates
    r^2 = a^2 cos 2 theta
This solution uses the polar parametric form.
'''

a = 2
t = np.linspace(0, 2*np.pi, 200)
sint = np.sin(t)
cost = np.cos(t)
theta = np.arctan2(sint*cost, cost)
r = a*np.abs(cost) / np.sqrt(1   sint**2)


fig, ax = plt.subplots(subplot_kw={'projection': 'polar'})
ax.plot(theta, r)

ax.set_rlabel_position(90)
ax.grid(True)

ax.set_title("A line plot on a polar axis", va='bottom')
plt.show()

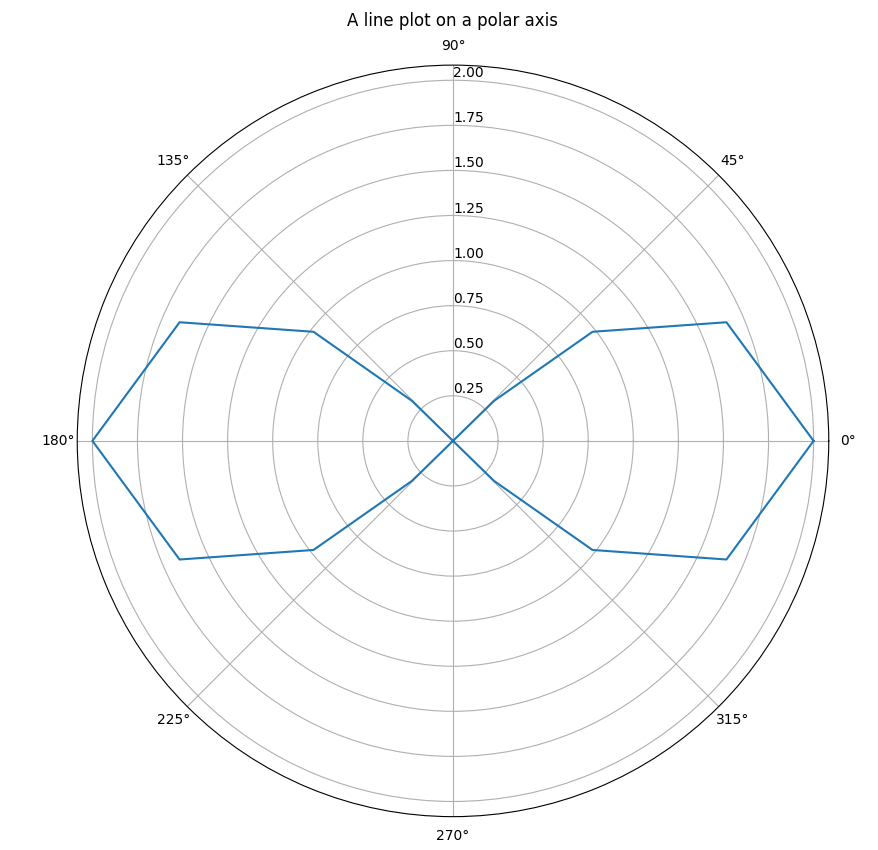
To illustrate how this handles edge conditions well, decrease the resolution of linspace to perhaps 15: