Matrix Subset Operations in Array-CodePudding

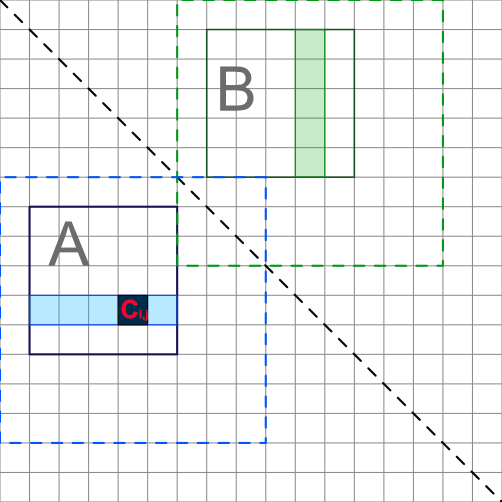
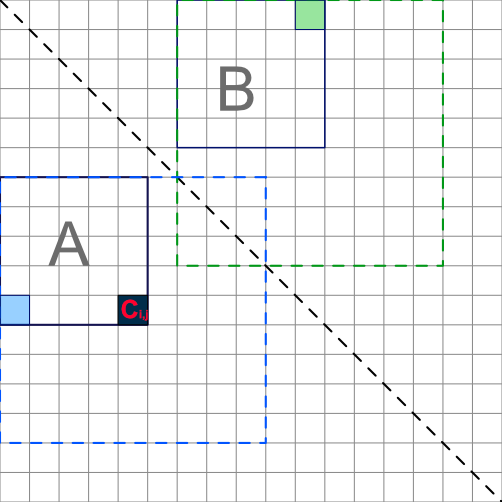
I have a matrix multiplication problem. We have an image matrix which can be have variable size. It is required to calculate C = A*B for every possible nxn. C will be added to output image as seen in figure. The center point of A Matrix is located in the lower triangle. Also, B is placed diagonally symmetric to A. A can be overlap, so, B can be overlap too. Figures can be seen in below for more detailed understand:

Blue X points represent all possible mid points of A. Algorithm should just do multiply A and diagonally mirrored version of A or called B. I done it with lots of for loop. I need to reduce number of for that I used. Could you help me please?

What kind of algorithm can be used for this problem? I have some confusing points.

Could you please help me with your genius algorithm talents? Or could you direct me to an expert?

Original Questions is below:

Thanks.

Update:

#define SIZE_ARRAY 20
#define SIZE_WINDOW 5
#define WINDOW_OFFSET 2
#define INDEX_OFFSET 1
#define START_OFFSET_COLUMN 2
#define START_OFFSET_ROW 3
#define END_OFFSET_COLUMN 3
#define END_OFFSET_ROW 2
#define GET_LOWER_DIAGONAL_INDEX_MIN_ROW (START_OFFSET_ROW);
#define GET_LOWER_DIAGONAL_INDEX_MAX_ROW (SIZE_ARRAY - INDEX_OFFSET - END_OFFSET_ROW)
#define GET_LOWER_DIAGONAL_INDEX_MIN_COL (START_OFFSET_COLUMN);
#define GET_LOWER_DIAGONAL_INDEX_MAX_COL (SIZE_ARRAY - INDEX_OFFSET - END_OFFSET_COLUMN)
uint32_t lowerDiagonalIndexMinRow = GET_LOWER_DIAGONAL_INDEX_MIN_ROW;
uint32_t lowerDiagonalIndexMaxRow = GET_LOWER_DIAGONAL_INDEX_MAX_ROW;
uint32_t lowerDiagonalIndexMinCol = GET_LOWER_DIAGONAL_INDEX_MIN_COL;
uint32_t lowerDiagonalIndexMaxCol = GET_LOWER_DIAGONAL_INDEX_MAX_COL;
void parallelMultiplication_Stable_Master()
{
    startTimeStamp = omp_get_wtime();

    #pragma omp parallel for num_threads(8) private(outerIterRow, outerIterCol,rA,cA,rB,cB) shared(inputImage, outputImage)
    for(outerIterRow = lowerDiagonalIndexMinRow; outerIterRow < lowerDiagonalIndexMaxRow; outerIterRow  )
    {
        for(outerIterCol = lowerDiagonalIndexMinCol; outerIterCol < lowerDiagonalIndexMaxCol; outerIterCol  )
        {
            if(outerIterCol   1 < outerIterRow)
            {
                rA = outerIterRow - WINDOW_OFFSET;
                cA = outerIterCol - WINDOW_OFFSET;

                rB = outerIterCol - WINDOW_OFFSET;
                cB = outerIterRow - WINDOW_OFFSET;

                for(i= outerIterRow - WINDOW_OFFSET; i <= outerIterRow   WINDOW_OFFSET; i  )
                {
                    for(j= outerIterCol - WINDOW_OFFSET; j <= outerIterCol   WINDOW_OFFSET; j  )
                    {
                        for(k=0; k < SIZE_WINDOW; k  )
                        {
                            #pragma omp critical
                            outputImage[i][j]  = inputImage[rA][cA k] * inputImage[rB k][cB];
                        }
                        cB  ;
                        rA  ;
                    }
                    rB  ;
                    cA  ;
                    printf("Thread Number - %d",omp_get_thread_num());
                }
            }
        }
    }
    stopTimeStamp = omp_get_wtime();
    printArray(outputImage,"Output Image");
    printConsoleNotification(100, startTimeStamp, stopTimeStamp);
}

I am getting segmentation fault error if I set up thread count more than "1". What is the trick ?

CodePudding user response：

I'm not providing a solution, but some thoughts that may help the OP exploring a possible approach.

You can evaluate each element of the resulting C matrix directly, from the values of the original matrix in a way similar to a

Instead of computing each matrix product for every A submatrix, you can evaluate the value of each C_{i, j} from the values in the shaded areas.

Note that C_{i, j} depends only on a small subset of row i and that the elements of the upper right triangular submatrix (where the B submatrices are picked) could be copied and maybe transposed in a more chache-friendly accomodation.

Alternatively, it may be worth exploring an approach where for every possible B_{i, j}, all the corresponding elements of C are evaluated.

edit

Note that you can actually save a lot of calculations (and maybe cache misses) by grouping the terms, see e.g. the first two elements of row i in A:

CodePudding user response：

Here is my take. I wrote this before OP showed any code, so I'm not following any of their code patterns.

I start with a suitable image struct, just for my own sanity.

struct Image
{
    float* values;
    int rows, cols;
};

struct Image image_allocate(int rows, int cols)
{
    struct Image rtrn;
    rtrn.rows = rows;
    rtrn.cols = cols;
    rtrn.values = malloc(sizeof(float) * rows * cols);
    return rtrn;
}
void image_fill(struct Image* img)
{
    ptrdiff_t row, col;
    for(row = 0; row < img->rows;   row)
        for(col = 0; col < img->cols;   col)
            img->values[row * img->cols   col] = rand() * (1.f / RAND_MAX);
}
void image_print(const struct Image* img)
{
    ptrdiff_t row, col;
    for(row = 0; row < img->rows;   row) {
        for(col = 0; col < img->cols;   col)
            printf("%.3f ", img->values[row * img->cols   col]);
        putchar('\n');
    }
    putchar('\n');
}

A 5x5 matrix multiplication is too small to reasonably dispatch to BLAS. So I write a simple version myself that can be loop-unrolled and / or inlined. This routine could use a couple of micro-optimizations but let's keep it simple for now.

/** out  = left * right for 5x5 sub-matrices */
static void mat_mul_5x5(
    float* restrict out, const float* left, const float* right, int cols)
{
    ptrdiff_t row, col, inner;
    float sum;
    for(row = 0; row < 5;   row) {
        for(col = 0; col < 5;   col) {
            sum = out[row * cols   col];
            for(inner = 0; inner < 5;   inner)
                sum  = left[row * cols   inner] * right[inner * cols   row];
            out[row * cols   col] = sum;
        }
    }
}

Now for the single-threaded implementation of the main algorithm. Again, nothing fancy. We just iterate over the lower triangular matrix, excluding the diagonal. I keep track of the top-left corner instead of the center point. Makes index computation a bit simpler.

void compute_ltr(struct Image* restrict out, const struct Image* in)
{
    ptrdiff_t top, left, end;
    /* if image is not quadratic, find quadratic subset */
    end = out->rows < out->cols ? out->rows : out->cols;
    assert(in->rows == out->rows && in->cols == out->cols);
    memset(out->values, 0, sizeof(float) * out->rows * out->cols);
    for(top = 1; top <= end - 5;   top)
        for(left = 0; left < top;   left)
            mat_mul_5x5(out->values   top * out->cols   left,
                        in->values   top * in->cols   left,
                        in->values   left * in->cols   top,
                        in->cols);
}

The parallelization is a bit tricky because we have to make sure the threads don't overlap in their output matrices. A critical section, atomics or similar stuff would cost too much performance.

A simpler solution is a strided approach: If we always keep the threads 5 rows apart, they cannot interfere. So we simply compute every fifth row, synchronize all threads, then compute the next set of rows, five apart, and so on.

void compute_ltr_parallel(struct Image* restrict out, const struct Image* in)
{
    /* if image is not quadratic, find quadratic subset */
    const ptrdiff_t end = out->rows < out->cols ? out->rows : out->cols;
    assert(in->rows == out->rows && in->cols == out->cols);
    memset(out->values, 0, sizeof(float) * out->rows * out->cols);
    /*
     * Keep the parallel section open for multiple loops to reduce
     * overhead
     */
#   pragma omp parallel
    {
        ptrdiff_t top, left, offset;
        for(offset = 0; offset < 5;   offset) {
            /* Use dynamic scheduling because the work per row varies */
#           pragma omp for schedule(dynamic)
            for(top = 1   offset; top <= end - 5; top  = 5)
                for(left = 0; left < top;   left)
                    mat_mul_5x5(out->values   top * out->cols   left,
                                in->values   top * in->cols   left,
                                in->values   left * in->cols   top,
                                in->cols);
        }
    }
}

My benchmark with 1000 iterations of a 1000x1000 image show 7 seconds for the serial version and 1.2 seconds for the parallelized version on my 8 core / 16 thread CPU.

EDIT for completeness: Here are the includes and the main for benchmarking.

#include <assert.h>
#include <stddef.h>
/* using ptrdiff_t */
#include <stdlib.h>
/* using malloc */
#include <stdio.h>
/* using printf */
#include <string.h>
/* using memset */

/* Insert code from above here */

int main()
{
    int rows = 1000, cols = 1000, rep = 1000;
    struct Image in, out;
    in = image_allocate(rows, cols);
    out = image_allocate(rows, cols);
    image_fill(&in);
# if 1
    do
        compute_ltr_parallel(&out, &in);
    while(--rep);
# else
    do
        compute_ltr(&out, &in);
    while(--rep);
# endif
}

Compile with gcc -O3 -fopenmp.

Regarding the comment, and also your way of using OpenMP: Don't overcomplicate things with unnecessary directives. OpenMP can figure out how many threads are available itself. And private variables can easily be declared within the parallel section (usually).

If you want a specific number of threads, just call with the appropriate environment variable, e.g. on Linux call OMP_NUM_THREADS=8 ./executable