Design polygons area in coord

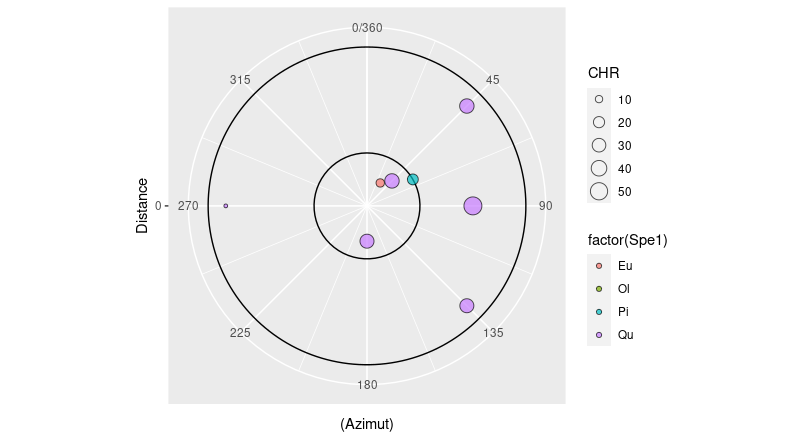
It happens that I'm carrying out surveys whose data can be shown directly (as if it were a map) using polar_coordinates as they are defined by the distance and angle with respect to the center. However, some data should be represented by not simple points but surfaces, defined by the position and angle of four or more points identified by a common variable (as would happen in a normal clustering). In the following example, I would like all the points identified with the variable "Qu" to be grouped on the same surface. The problem of calculating the surfaces can easily be tackled separately, for the purposes of the graph for the moment I am only interested in the representation.

library(ggplot2)

Azimut<-c(30,60,90,270,275, 45, 135, 45, 180)
Distance<-c(3,6,12,16,22, 4, 16, 18, 18)
CHR<-c(12,19,55,7,39,34,32,34,32)
Spe1<-c("Eu","Pi","Qu","Qu","Ol", "Qu", "Qu", "Qu", "Qu")
Tr1<-data.frame(Azimut,Distance, CHR, Spe1)
Tr1$Theta<-2*pi*Azimut/360

# With polar coordinates
ggplot(aes(x = (Azimut), y = Distance), data = Tr1)   
  geom_hline(aes(yintercept = 6))  
  geom_hline(aes(yintercept = 18))  
  scale_x_continuous(limits = c(0, 360),
                     breaks = seq(0, 360, 45))  
  scale_y_continuous(limits = (c(0, 18)),
                     breaks = (seq(0, 6, 18)))  
  geom_point(aes(size=CHR, fill=factor(Spe1)),shape =21,alpha = 0.7) 
  coord_polar(theta = "x")

That gives this result:

CodePudding user response：

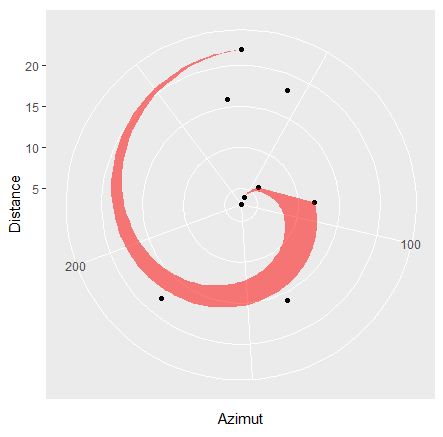
You can find the row indices of the points forming a surrounding convex hull with chull and use their coordinates with geom_polygon. With cartesian coordinates this works - but polar coordinates may give unexpected results. In case of your example data:

library(ggplot2)
library(dplyr)

df <- 
  data.frame(
    Azimut = c(30,60,90,270,275, 45, 135, 45, 180),
    Distance = c(3,6,12,16,22, 4, 16, 18, 18),
    CHR = c(12,19,55,7,39,34,32,34,32),
    Spel = c("Eu","Pi","Qu","Qu","Ol", "Qu", "Qu", "Qu", "Qu")
  ) |>
  mutate(Theta =  pi * Azimut / 180)
  
## which rows of subset Spel === "Qu" form the convex hull for this subset
hull_rows <- 
  df |>
  filter(Spel == "Qu") |>
  select(Azimut, Distance) |>
  chull()

df |>
  ggplot()  
  geom_point(aes(Azimut, Distance))  
  geom_polygon(data = df[hull_rows,],
               aes(Azimut, Distance),
               fill = 'red', alpha = .5
               )   coord_polar()

(kind of Debian logo ...)

CodePudding user response：

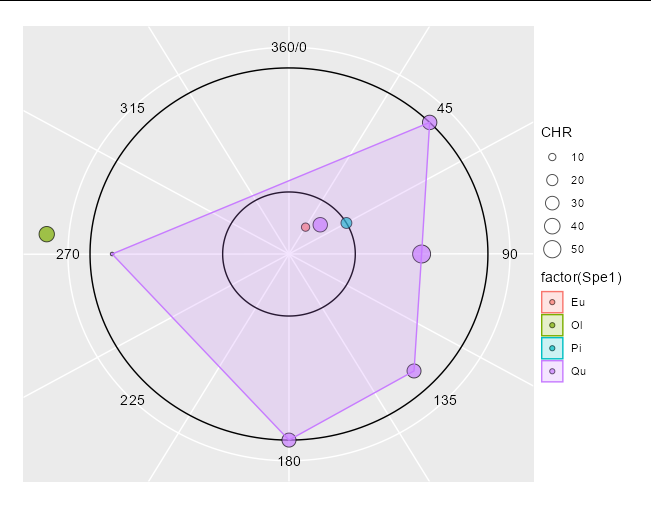
You have two options here. One is to calculate the curves that, when transformed to polar co-ordinates, give straight lines. The second is to convert your data to polar co-ordinates and plot normal rectilinear polygons. For several reasons, I think the second option is easier. It is even possible to use annotation layers to fake the polar axes:

library(ggplot2)

ggplot(aes(x = Distance * cos(Theta), y = Distance * sin(Theta)), data = Tr1)  
  geom_abline(slope = c(1000, 0, tan(pi/6), tan(pi/3), tan(-pi/3), tan(-pi/6)),
              color = 'white', linewidth = 0.5)  
  geom_path(aes(x = x, y = y), 
            data = data.frame(x = 6 * sin(seq(0, 2 * pi, length = 200)),
                              y = 6 * cos(seq(0, 2 * pi, length = 200))))  
  geom_path(aes(x = x, y = y), 
            data = data.frame(x = 18 * sin(seq(0, 2 * pi, length = 200)),
                              y = 18 * cos(seq(0, 2 * pi, length = 200))))  
  geom_path(aes(x = x, y = y), 
            data = data.frame(x = 20 * sin(seq(0, 2 * pi, length = 200)),
                              y = 20 * cos(seq(0, 2 * pi, length = 200))),
            col = 'white')  
  annotate("text", label = c("360/0", seq(45, 315, 45)),
           x = 20 * sin(seq(pi/2, -5*pi/4, -pi/4)),
           y = 20 * cos(seq(pi/2, -5*pi/4, -pi/4)))  
  geom_point(aes(size = CHR, fill = factor(Spe1)), shape = 21, alpha = 0.7)  
  lapply(split(Tr1, Tr1$Spe1), function(x) {
    if(nrow(x) < 4) return(NULL)
    geom_polygon(data = x[chull(x$Distance * cos(x$Theta), 
                                x$Distance * sin(x$Theta)),],
                 aes(fill = factor(Spe1), 
                     color = after_scale(scales::alpha(fill, 1))), alpha = 0.2)
  })  
  coord_flip()  
  theme_void()  
  theme(panel.background = element_rect(fill = 'gray92', color = NA),
        plot.margin = margin(20, 20, 20, 20))