Principal Component Analysis in R by hand-CodePudding

The questions is about Principal Component Analysis, partly done by hand.

Disclaimer: My background is not in maths and I am using R for the first time.

Given are the following five data points in R^3. Where xi1-3 are variables and x1 - x5 are observations.

    | x1 x2 x3 x4 x5 
----------------------
xi1 | -2 -2  0  2  2 
xi2 | -2  2  0 -2  2 
xi3 | -4  0  0  0  4

Three principal component vectors after the principal component analysis has been performed are given, and look like this:

Phi1 = (0.41, 0.41, 0.82)T
Phi2 = (-0.71, 0.71, 0.00)T
Phi3 = (0.58, 0.58, -0.58)T

The questions are as follows

1) Calculate the principal component scores zi1, zi2 and zi3 for each of the 5 data points.
2) Calculate the proportion of the variance explained by each principal component.

So far I have answered question 1 with the following code, where Z represents the scores:

A = matrix(
c(-2, -2, 0, 2, 2, -2, 2, 0, -2, 2, -4, 0, 0, 0, 4),
nrow = 3,
ncol = 5,
byrow = TRUE
)

Phi = matrix (
c(0.41, -0.71, 0.58,0.41, 0.71, 0.58, 0.82, 0.00, -0.58),
nrow = 3,
ncol = 3,
byrow = FALSE
)

Z = Phi%*%A

Now I am stuck with question 2, I am given the formula:

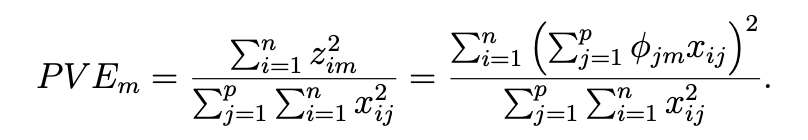
But I am not sure how I can recreate the formula with an R command, can anyone help me?

CodePudding user response：

#Here is the numerator:
(Phi%*%A)^2%>%rowSums()
[1] 48.4128 16.1312  0.0000

#Here is the denominator:
sum(A^2)
[1] 64

#So the answer is:
(Phi%*%A)^2%>%rowSums()/sum(A^2)
[1] 0.75645 0.25205 0.00000

we can verify with prcomp summary:

summary(prcomp(t(A)))

Importance of components:
                         PC1  PC2 PC3
Standard deviation     3.464 2.00   0
Proportion of Variance 0.750 0.25   0
Cumulative Proportion  0.750 1.00   1

This is roughly the same since your $\Phi$ is rounded to two decimals.