find tangent line of two adjacent circle-CodePudding

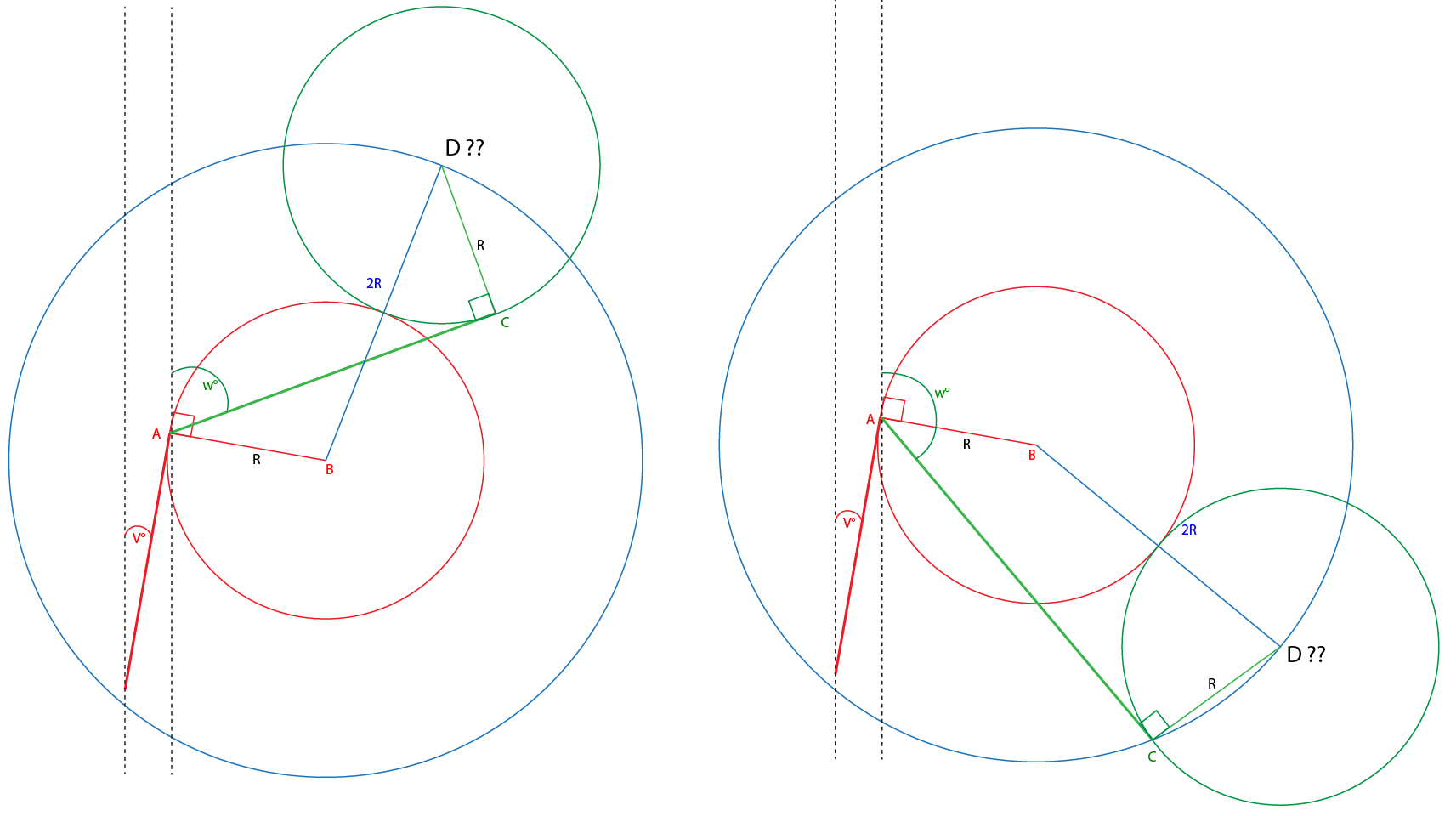
those are 2 example cases of what I need to solve, it is just finding the coordinate of D, given position of A, and the direction vector of red and green line

red/green line vector (or direction) is known
point A is an intersection between the red line and red circle tangent point
point B is the center of the red circle with radius = R (known)
point C is an intersection between the green line and the green circle tangent point
point D is unknown and this one that needs to be calculated
point D will always located in green circle (radius of 2R from point B)
both red and green line has the same radius of R
V is the angle of the red line relative to north up
W is the angle of the green line relative to north up
the distance between point B and D is always 2R since the circle adjacent (touching each other)

much help and hint appreciated, preferred in some code instead of math equation

CodePudding user response：

Having coordinates A,B,C, we can write two vector equations using scalar (dot) product:

AC.dot.DC = 0
DB.dot.DB = 4*R^2

The first one refers to perpendicularity between tangent to circle and radius to tangency point, the second one - just squared distance between circle centers.

In coordinates:

(cx-ax)*(cx-dx)   (cy-ay)*(cy-dy) = 0
(bx-dx)*(bx-dx)   (by-dy)*(by-dy) = 4*R^2

Solve this system for unknown dx, dy - two solutions in general case.

If A and C are not known, as @Mike 'Pomax' Kamermans noticed:

Let

cr = sin(v)     sr = cos(v)
cg = sin(w)     sg = cos(w)

ax = bx   R * cr
ay = by   R * sr

and

dx = cx - R * cg
dy = cy   R * sg

Substituting expressions into the system above we have:

(dx R*cg-bx-R*cr)*cg - (dy-R*sg-by-R*sr)*sg = 0
(bx-dx)*(bx-dx)   (by-dy)*(by-dy) = 4*R^2

Again - solve system for unknowns dx, dy

CodePudding user response：

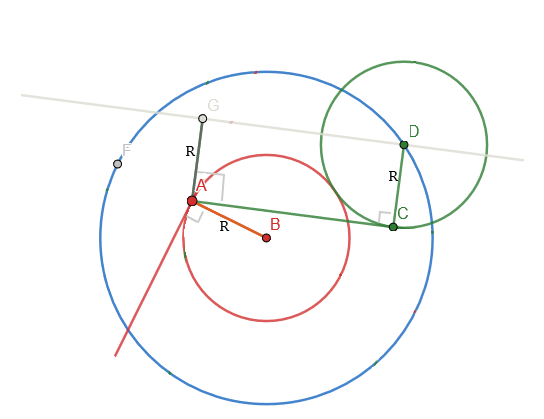
As a hint: draw it out some more:

We can construct D by constructing the line segment AG, for which we know both the angle and length, because AC⟂AG, and the segment has length R.

We can then construct a line perpendicular to AG, through G, which gives us a chord on the blue circle, one endpoint of which is D. We know the distance from B to GD (because we know trigonometry) and we know that the distance BD is 2R (because that's a given). Pythagoras then trivially gives us D.