import numpy as np
 from time import time
 import matplotlib.pyplot as plt
 np.random.seed(27)


 mysetup = "from math import sqrt"

 begin=time()
 i=int(input("Number of rows in first matrix"))
 k=int(input("Number of column in first and rows in second matrix"))
 j=int(input("Number of columns in second matrix"))
 A = np.random.randint(1,10,size = (i,k))
 B = np.random.randint(1,10,size = (k,j))
 
 
 
 
def multiply_matrix(A,B):
    global C
    if A.shape[1]==B.shape[0]:
     C=np.zeros((A.shape[0],B.shape[1]),dtype=int)
     for row in range(i):
        for col in range(j):
            for elt in range(0,len(B)):
                C[row,col]  = A[row,elt]*B[elt,col]
     return C
         
    else:
          return  "Cannot multiply A and B"

print(f"Matrix A:\n {A}\n")
print(f"Matrix B:\n {B}\n")
D=print(multiply_matrix(A, B))

end=time()
t=print(end-begin)
x=[0,100,10]
y=[100,100,1000]
plt.plot(x,y)
plt.xlabel('Time taken for the program to run')
plt.ylabel('Order of the matrix multiplication')
plt.show()  

In the program, I have generated random elements for the matrices to be multiplied.Basically I am trying to compute the time it takes to multiply two matrices.The i,j and k will be considered as the order used for the matrix.As we cannot multiply matrices where number of columns of the first is not equal to the number of the rows in the second, I have already given them the variable 'k'. Initially I considered to increment the order of the matrix using for loop but wasn't able to do so. I want the graph to display the time it took to multiply the matrices on the x axis and the order of the resultant matrix on the y axis. There is a problem in the logic I applied but I am not able to find out how to do this problem as I am a beginner in programming I was expecting to get the result as Y axis having a scale ranging from 0 to 100 with a difference of 10 and x axis with a scale of 100 to 1000 with a difference of 100. The thousandth entity on the x axis will correspond to the time it took to compute the multiplication of two matrices with numbers of rows and columns as 1000. Suppose the time it took to compute this was 200seconds. So the graph should be showing the point(1000,200).

CodePudding user response：

Some problematic points I'd like to address -

1. You're starting the timer before the user chooses an input - which can differ, we want to be as precise as possible, thus we need to only calculate how much time it takes for the multiply_matrix function to run.
2. Because you're taking an input - it means that each run you will get one result, and one result is only a single point - not a full graph, so we need to get rid of the user input and generate our own.
3. Moreover to point #2 - we are not interested in giving "one shot" for each matrix order - that means that when we want to test how much time it takes to multiply two matrices of order 300 (for example) - we need to do it N times and take the average in order to be more precise, not to mention we are generating random numbers, and it is possible that some random generated matrices will be easier to compute than other... although taking the average over N tests is not 100% accurate - it does help.
4. You don't need to set C as a global variable as it can be a local variable of the function multiply_matrix that we anyways return. Also this is not the usage of globals as even with the global C - it will be undefined in the module level.
5. This is not a must, but it can improve a little bit your program - use time.perf_counter() as it uses the clock with the highest (available) resolution to measure a short duration, and it avoids precision loss by the float type.
6. You need to change the axes because we want to see how the time is affected by the order of the matrices, not the opposite! (so our X axis is now the order and the Y is the average time it took to multiply them)

Those fixes translate to this code:

1. Calculating how much it takes for multiply_matrix only.

begin = time.perf_counter()
C = multiply_matrix(A, B)
end = time.perf_counter()

2 3. Generating our own data, looping from order 1 to order maximum_order, taking 50 tests for each order:

maximum_order = 50
tests_number_for_each_order = 50

def generate_matrices_to_graph():
    matrix_orders = []  # our X
    multiply_average_time = []  # our Y

    for order in range(1, maximum_order):
        print(order)
        times_for_each_order = []
        for _ in range(tests_amount_for_each_order):
            # generating random square matrices of size order.
            A = np.random.randint(1, 10, size=(order, order))
            B = np.random.randint(1, 10, size=(order, order))

            # getting the time it took to compute
            begin = time.perf_counter()
            multiply_matrix(A, B)
            end = time.perf_counter()

            # adding it to the times list
            times_for_each_order.append(end - begin)

        # adding the data about the order and the average time it took to compute
        matrix_orders.append(order)
        multiply_average_time.append(sum(times_for_each_order) / tests_amount_for_each_order)  # average
    return matrix_orders, multiply_average_time

4. Minor changes to multiply_matrix as we don't need i, j, k from the user:

def multiply_matrix(A, B):

    matrix_order = A.shape[1]

    C = np.zeros((matrix_order, matrix_order), dtype=int)
    for row in range(matrix_order):
        for col in range(matrix_order):
            for elt in range(0, len(B)):
                C[row, col]  = A[row, elt] * B[elt, col]
    return C

and finally call generate_matrices_to_graph

# calling the generate_data_and_compute function
plt.plot(*generate_matrices_to_graph())
plt.xlabel('Matrix order')
plt.ylabel('Time [in seconds]')
plt.show()

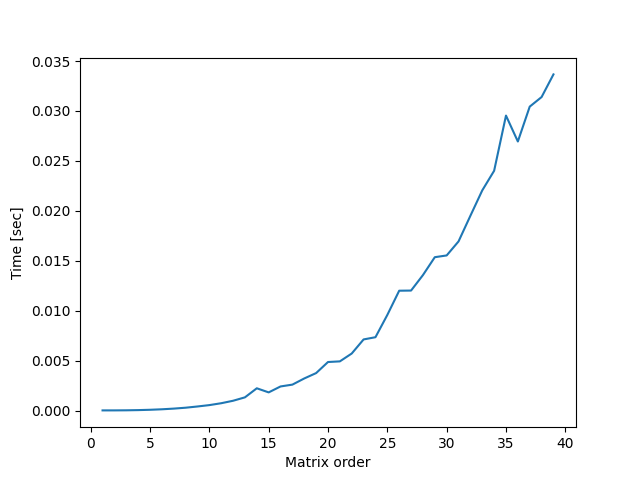
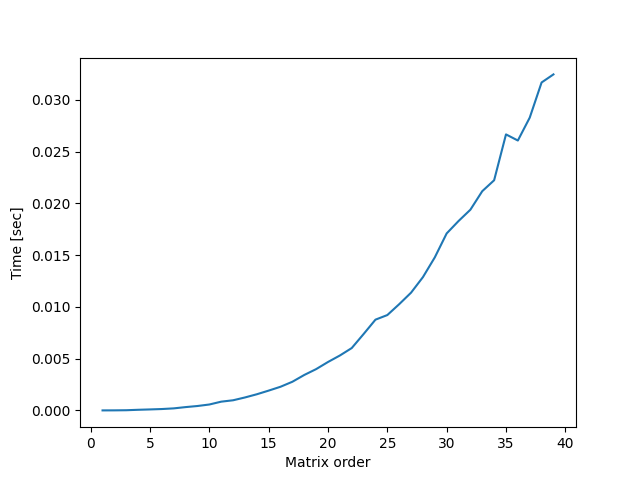
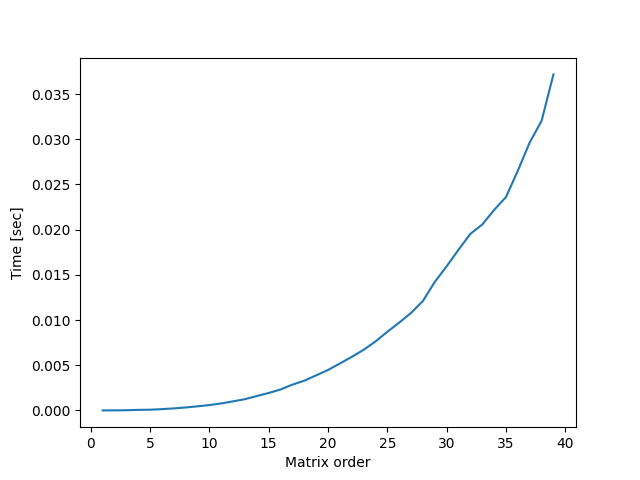
Some outputs:

We can see that when our tests_number_for_each_order is small, the graph loses precision and crisp.

Going from order 1-40 with 1 test for each order:

Going from order 1-40 with 30 tests for each order:

Going from order 1-40 with 80 tests for each order:

CodePudding user response：

I love this kind of questions:

import numpy as np
from time import time
import matplotlib.pyplot as plt
np.random.seed(27)

dim = []
times = []
for i in range(1,10001,10):
    A = np.random.randint(1,10,size=(1,i))
    B = np.random.randint(1,10,size=(i,1))
    begin = time()
    C = A*B
    times.append(time()-begin)
    dim.append(i)


plt.plot(times,dim)

This is a simplified test in which I tested 1 dimension matrices, (1,1)(1,1), (1,10)(10,1), (1,20)(20,1) and so on... But you can make a double iteration to change also the "outer" dimension of the matrices and see how this affect the computational time