MATLAB error using fzero function to solve the loop-CodePudding

My following code generates the plot of V and D values in figure 1. In the graph, the parabolas and straigh lines intersect, and I need to find the roots from the plot from a loop. So I tried to use fzero function, but the error appeared:

Operands to the logical AND (&&) and OR (||) operators must be convertible to logical scalar values. Use the ANY or ALL functions to reduce operands to logical scalar values.

Error in fzero (line 326)
elseif ~isfinite(fx) || ~isreal(fx)

Error in HW1 (line 35)
x=fzero(fun,1);

My code is:

clear all; close all

W = 10000; %[N]
S = 40; %[m^2]
AR = 7;
cd0 = 0.01;
k = 1 / pi / AR;
clalpha = 2*pi;
Tsl=800; 
figure(1);hold on; xlabel('V');ylabel('D')
for h=0:1:8; 
    i=0;
    for alpha = 1:0.25:12
        i=i 1;
        rho(i)=1.2*exp(-h/10.4);
        cl(i) = clalpha * alpha * pi/180;
        V(i) = sqrt(2*W/rho(i)/S/cl(i));
        L(i) = 0.5 * rho(i) * V(i) * V(i) * S * cl(i);
        cd(i) = cd0   k * cl(i) * cl(i);
        D(i) = 0.5 * rho(i) * V(i) * V(i) * S * cd(i);
        clcd(i) = cl(i)/cd(i);
        p(i) = D(i)*V(i);
        ang(i) = alpha;
        T(i)=Tsl*(rho(i)/1.2).^0.75;
    end
    figure(1); plot(V,D); hold on 
    plot(V,T);
end
fun = @(V) 0.5*V.*V.*rho.*S.*cd-T;
x=fzero(fun,1);

Probably, I should not use the fzero function, but the task is to find the roots of V from a plot (figure 1). There are parabolas and straight lines respectively.

CodePudding user response：

From the documentation for fzero(fun,x)

fun: Function to solve, specified as a handle to a scalar-valued function or the name of such a function. fun accepts a scalar x and returns a scalar fun(x).

Your function does not return a scalar value for a scalar input, it always returns a vector which is not valid for a function which is being used with fzero.

CodePudding user response：

1.- Your codes doesn't plot V and D: Your code plots D(V) and T(V)

2.- T is completely flat, despite taking part in the inner for loop calculations with T(i)=Tsl*(rho(i)/1.2).^0.75; as it had to be somehow modified.

But in fact it remains constant for all samples of V, constant temperature (°C ?), and for all laps of the outer for loop sweeping variable h within [0:1:8].

The produced T(V) functions are the flat lines.

3.- Then you try building a 3rd function f that you put as if f(V) only but in fact it's f(V,T) with the right hand side of the function with a numerical expression, without a symbolic expression, the symbolic expression that fzero expects to attempt zero solving.

In MATLAB Zero finding has to be done either symbolically or numerically.

A symbolic zero-finding function like fzero doesn't work with numerical expressions like the ones you have calculated throughout the 2 loops for h and for alpha .

Examples of function expressions solvable by fzero :

3.1.-

fun = @(x)sin(cosh(x));
x0 = 1;
options = optimset('PlotFcns',{@optimplotx,@optimplotfval});
x = fzero(fun,x0,options)

3.2.-

fun = @sin; % function
x0 = 3; % initial point
x = fzero(fun,x0)

3.3.- put the following 3 lines in a separate file, call this file f.m

function y = f(x)
y = x.^3 - 2*x - 5;

and solve

fun = @f; % function
x0 = 2; % initial point
z = fzero(fun,x0)

3.4.- fzeros can solve parametrically

myfun = @(x,c) cos(c*x);  % parameterized function
c = 2;                    % parameter
fun = @(x) myfun(x,c);    % function of x alone
x = fzero(fun,0.1)

4.- So since you have already done all the numerical calculations and no symbolic expression is supplied, it's reasonable to solve numerically, not symbolically.

To this purpose there's a really useful function called intersections.m written by Douglas Schwarz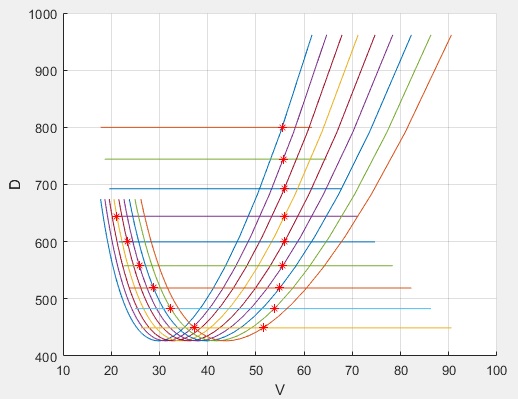

Because at each pair D(V) T(V) there may be no roots, 1 root or more than 1 root, it makes sense to use a cell, reczeros, to store whatever roots obtained.

To read obtained roots in let's say laps 3 and 5:

reczeros{3}
=
55.8850  692.5504
reczeros{5}
=
23.3517  599.5325
55.8657  599.5325

And now the 2nd graph, the function that is defined in a different way as done in the double for loop:

P = 0.5*V.*V.*rho.*S.*cd-T;

figure(2);
ax2=gca
hold(ax2,'on');xlabel(ax2,'V');ylabel(ax2,'P');grid(ax2,'on');
title(ax2,'2nd graph')
plot(ax2,V,P)
plot(ax2,V,T)

[x0,y0]=intersections1(V,T,V,P,'robust');
for k1=1:1:numel(x0)
    plot(ax2,x0,y0,'r*');hold(ax2,'on')
end

format short
V0=x0
P0=y0
V0 =
86.9993
P0 =
449.2990