How do I fit this curve?-CodePudding

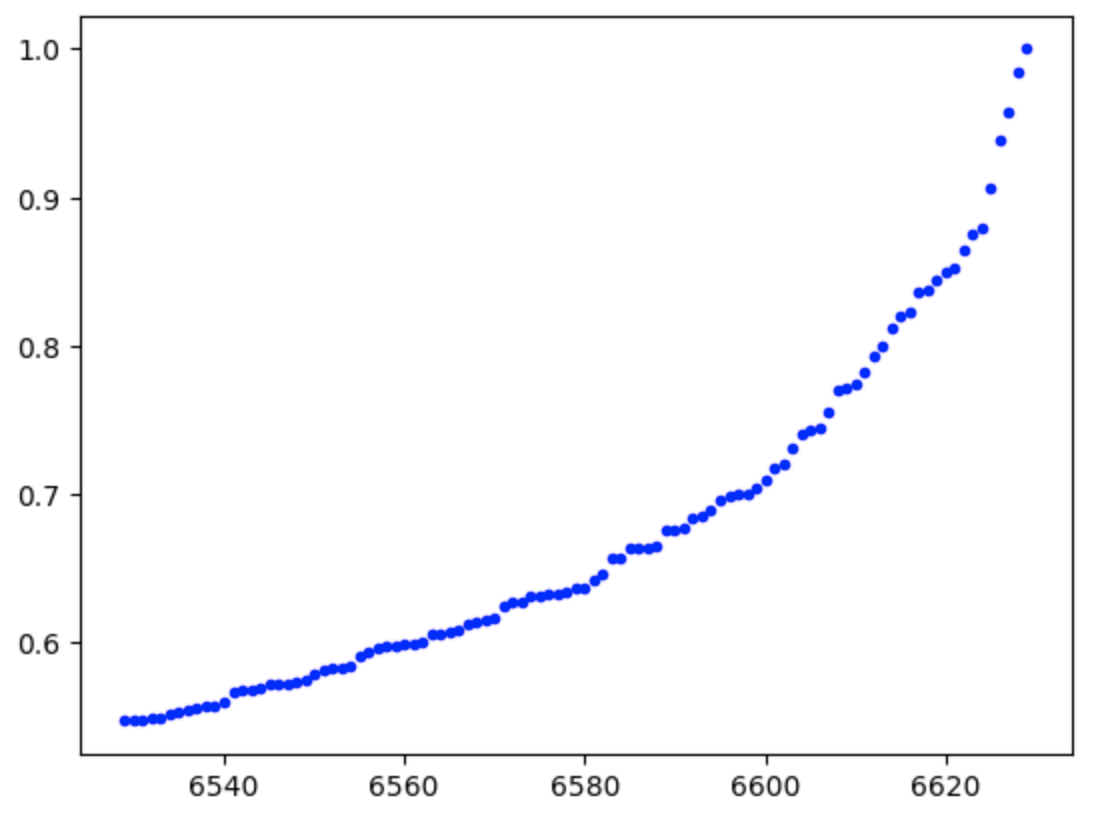
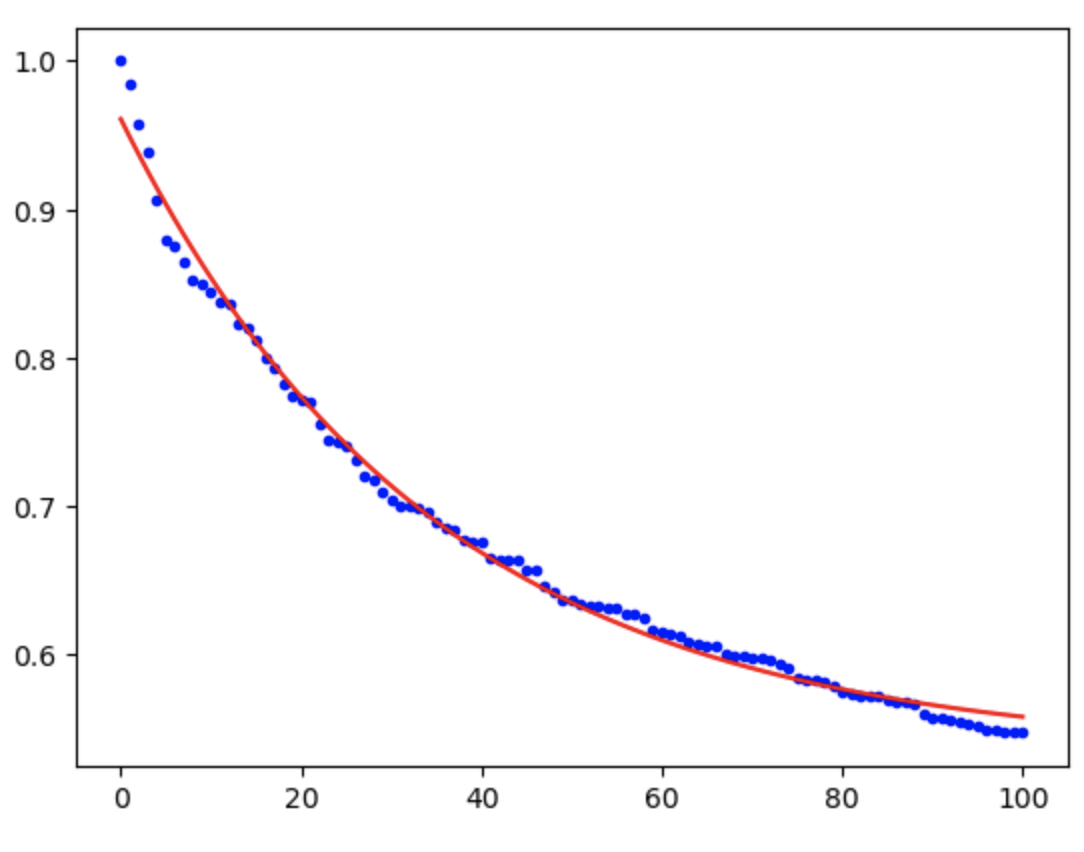
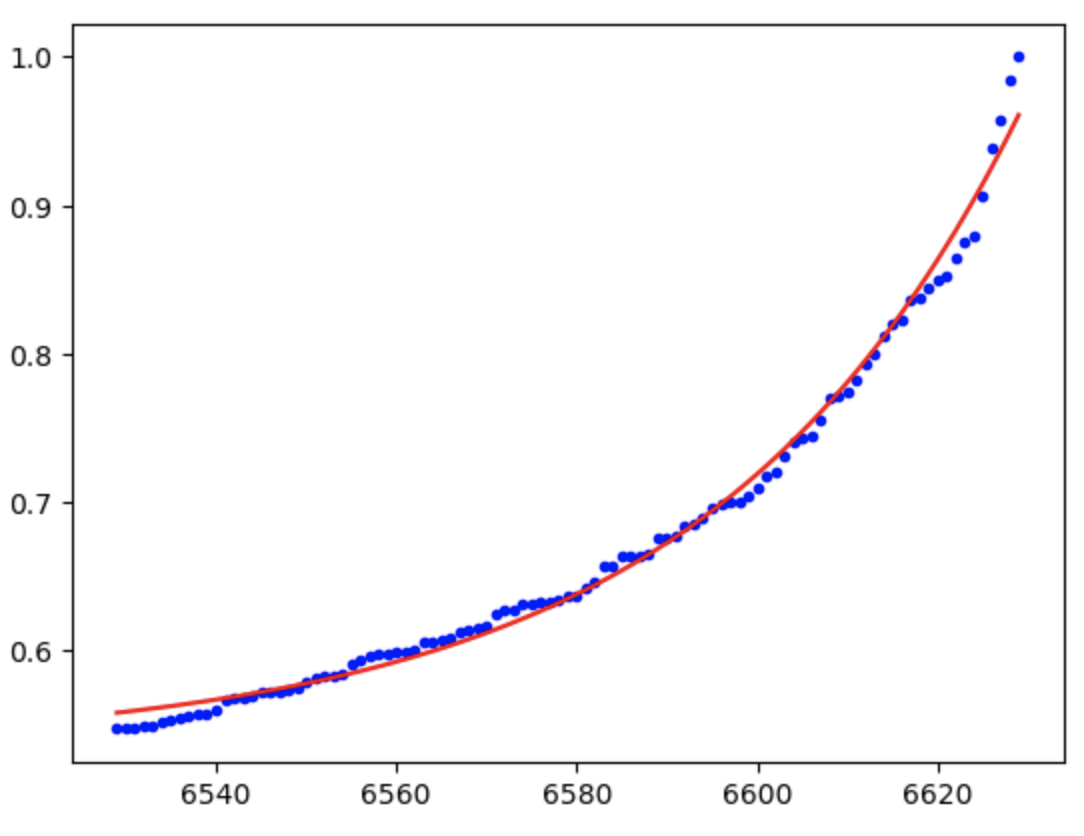
I am trying to find a function to model my curved dataset using scipy's curve fit function which gets me a line and spits out error message "OptimizeWarning: Covariance of the parameters could not be estimated"

This is my data:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit


def func(x, a, b, c):
    return a * np.exp(-b * x)   c

x = [6529,6530,6531,6532,6533,6534,6535,6536,6537,6538,6539,6540,6541,6542,6543,6544,6545,6546,6547,6548,6549,6550,6551,6552,6553,6554,6555,6556,6557,6558,6559,6560,6561,6562,6563,6564,6565,6566,6567,6568,6569,6570,6571,6572,6573,6574,6575,6576,6577,6578,6579,6580,6581,6582,6583,6584,6585,6586,6587,6588,6589,6590,6591,6592,6593,6594,6595,6596,6597,6598,6599,6600,6601,6602,6603,6604,6605,6606,6607,6608,6609,6610,6611,6612,6613,6614,6615,6616,6617,6618,6619,6620,6621,6622,6623,6624,6625,6626,6627,6628,6629]
xdata = np.array(x)
xdata

y =[0.547409184506862,0.548439334507089,0.548707663683029,0.549517457040911,0.549928046272648,0.552133076225856,0.553680404362389,0.554546610865359,0.556183559635298,0.55702393264449,0.558127603440548,0.56005701419833,0.567268696243044,0.567959158455945,0.56888383955428,0.570002946460703,0.571738099634388,0.571781066314887,0.572492904162659,0.573363360104158,0.575401312020501,0.579556244995718,0.581790310757611,0.583406644934125,0.583431253838386,0.584646128487338,0.591634693424932,0.593621181449664,0.596918227952608,0.597537299010122,0.597822020010253,0.598891783912097,0.599584877929425,0.600869677067233,0.605499427101361,0.60658392374002,0.607408603951367,0.608003672935112,0.612816417541406,0.614176393253985,0.615691612727725,0.617134841882831,0.624502603183639,0.627504005062751,0.62811483139368,0.630923224681103,0.631913519350306,0.632861774084856,0.633396927216081,0.634723100574364,0.636823036518848,0.637335872514631,0.641989703420432,0.645848889736627,0.65711344945379,0.657128729116295,0.663572015593525,0.663936607768306,0.664261916284895,0.665497047151865,0.675768594810369,0.676207425367557,0.67770213122942,0.684362066388147,0.686091459831405,0.68923449405901,0.696555953074396,0.699523852803358,0.700114629853266,0.700439968032363,0.70422912133774,0.709054418203755,0.718323675919034,0.720874110082631,0.731420313805414,0.740339970645214,0.743941832408661,0.744098264483215,0.755637715557576,0.770607412727517,0.772170144147719,0.77386595160397,0.782346429315201,0.793536926034814,0.799814727138212,0.811806170429752,0.820389958104833,0.823442687233217,0.836431157138314,0.837230603981482,0.84457830759536,0.849472002016762,0.853064650303987,0.864143132487712,0.875848713252245,0.879457500784825,0.906226501241044,0.938124902423877,0.957251151492073,0.984140865987764,1]
ydata = np.array(y)
ydata

plt.plot(xdata, ydata, 'b.', label='data')

I tried the curve_fit function

popt, pcov = curve_fit(func, xdata, ydata)
popt

plt.plot(xdata, func(xdata, *popt), 'r-',
         label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

but it just plots a horizontal line.

The closest I've gotten to this was using a linear regression model in R (something along the lines of model <- lm(log(y)~x, data=df) that looks like this:

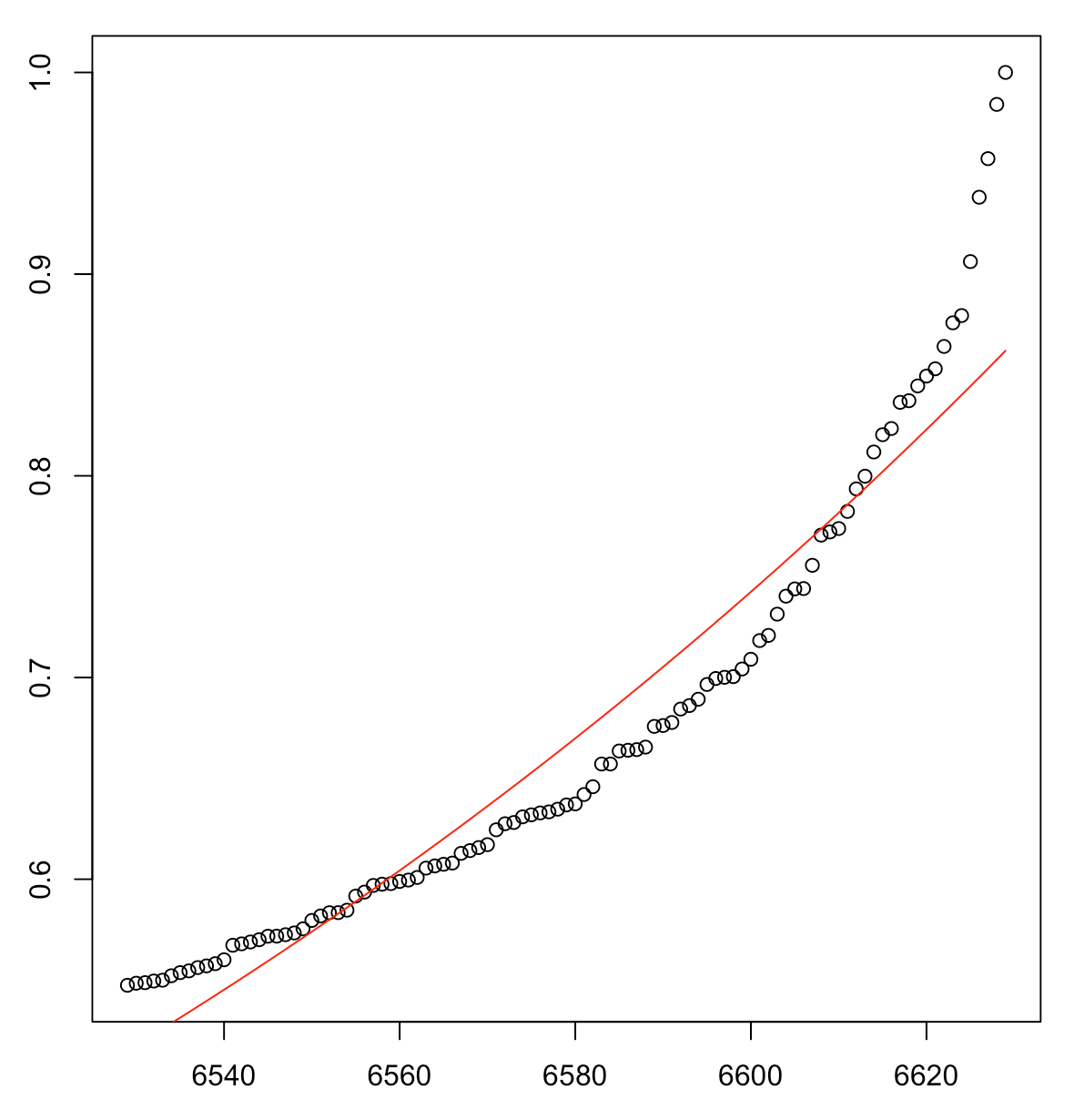
But I want it to look more like this:

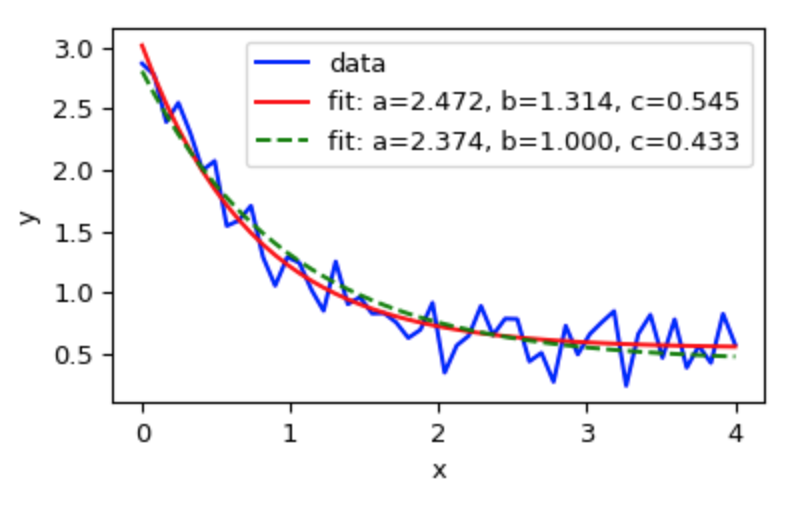
So that I can take the derivative of the curve afterwards. Sorry if my code is lacking, I'm new to python.

CodePudding user response：

You can use linear regression if you transform your data before you do the fit.

The function you want looks like this:

y = a*exp(b*x)

Take the natural log of both sides:

ln(y) = ln(a)   b*x

You can see this looks like a linear regression where the y-intercept is ln(a) and the slope is b.

You'll need to take the natural log of each term in the y-array before you do the linear regression.

When the calculation is done, you'll get the value for a by exp(ln(a)).

CodePudding user response：

You can apply a simple transformation to xdata:

max_xdata = xdata.max()
xdata_t = max_xdata - xdata

popt, pcov = curve_fit(func, xdata_t, ydata)
print(popt)

fix, ax = plt.subplots(1, 1)
ax.plot(xdata_t, ydata, 'b.', label='data')
ax.plot(xdata_t, func(xdata_t, *popt), 'r-',
         label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))

Which gets you:

Or, to get the fit to the original dataset:

fix, ax = plt.subplots(1, 1)
ax.plot(xdata, ydata, 'b.', label='data')
ax.plot(xdata, func(max_xdata - xdata, *popt), 'r-',
         label='fit: a=%5.3f, b=%5.3f, c=%5.3f' % tuple(popt))