Function vectorization says there is a 0-dimensional argument while the argument is an array-CodePudding

I'm implementing this equation and using it for the set of frequencies nos:

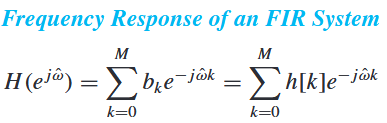
The non vectorized code works:

import numpy as np

h = np.array([1,2,3])
nos = np.array([4, 5, 6, 7])

func = lambda h, no: np.sum([hk * np.exp(-1j * no * k) for k, hk in enumerate(h)])

# Not vectorized
resps = np.zeros(nos.shape[0], dtype='complex')
for i, no in enumerate(nos):
    resps[i] = func(h, no)
print(resps)


> Out: array([-0.74378734-1.45446975j,
>             -0.94989022 3.54991188j,
>              5.45190245 2.16854975j,  
>              2.91801616-4.28579526j])

I'd like to vectorize the call in order to pass nos at once instead of explicitly iterating:

H = np.vectorize(func, excluded={'h'}, signature='(k),(n)->(n)')
resps = H(h, nos)

When calling H:

Error: ValueError: 0-dimensional argument does not have enough dimensions for all core dimensions ('n',)

I'm using the signature parameter but I'm not sure I use it in the correct way. Without this parameter there is an error in func:

TypeError: 'numpy.int32' object is not iterable

I don't understand where the problem is.

CodePudding user response：

A list comprehension version of your loop:

In [15]: np.array([func(h,n) for n in nos])
Out[15]: 
array([-0.74378734-1.45446975j, -0.94989022 3.54991188j,
        5.45190245 2.16854975j,  2.91801616-4.28579526j])

vectorize - excluding the first argument (by position, not name), and scalar iteration on second.

In [16]: f=np.vectorize(func, excluded=[0])    
In [17]: f(h,nos)
Out[17]: 
array([-0.74378734-1.45446975j, -0.94989022 3.54991188j,
        5.45190245 2.16854975j,  2.91801616-4.28579526j])

No need to use signature.

With true numpy vectorization (not the pseudo np.vectorize):

In [23]: np.sum(h * np.exp(-1j * nos[:,None] * np.arange(len(h))), axis=1)
Out[23]: 
array([-0.74378734-1.45446975j, -0.94989022 3.54991188j,
        5.45190245 2.16854975j,  2.91801616-4.28579526j])