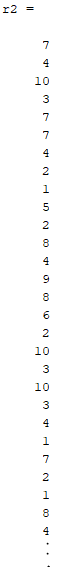Convert a vector to a symmetric hollow matrix in Matlab-CodePudding

I would like to convert a vector to a symmetric hollow matrix but I am not really familiar with Matlab.

For example:

r2 = randi(10,276,1);

and convert it into a symmetric hollow matrix, so a symmetric matrix about a diagonal of zeros (see image below for desired outcome). The output matrix should be 24x24 (276 276 24(zeros))

Thanks for your help!

CodePudding user response：

You can obtain your hollow matrix by iterating through the rows and columns, pasting in the desired elements of r2. Simplest is to keep track of where you are in r2 as you go. I'm sure there's some direct calculation that can be done with triangular numbers to get the r2Slice indices directly, if you need it.

r2 = randi(10,276,1);

% 1   inverse triangular number formula
numrows = 1 sqrt(2.*numel(r2) 1/4)-1/2;
mat = zeros(numrows);

firstelement = 1;
lastelement = numrows-1;
for i = 1:numrows-1
    r2Slice = r2(firstelement:lastelement);
    mat(i,i 1:end) = r2Slice';
    mat(i 1:end,i) = r2Slice;
    firstelement = lastelement 1;
    lastelement = lastelement numrows-1-i;
end

Edit: Since I couldn't get it out of my brain, here's the version with direct index calculation:

r2 = randi(10,276,1);

% triangular number formulas
triang = @(x)x.*(x 1)./2;
inv_triang = @(x)sqrt(2.*x 1/4)-1/2;

numrows = 1 inv_triang(numel(r2));
mat = zeros(numrows);

firstelement = @(i)triang(numrows-1)-triang(numrows-1-i 1) 1;
lastelement = @(i)firstelement(i) numrows-1-i;

for i = 1:numrows-1
    r2Slice = r2(firstelement(i):lastelement(i));
    mat(i,i 1:end) = r2Slice';
    mat(i 1:end,i) = r2Slice;
end

CodePudding user response：

Try this:

r2 = randi(10,24);
r2 = (r2 r2')./2; % make matrix symmetric by adding transpose and divide by 2
r2 = r2 - diag(diag(r2)); % subtract diagonal matrix with diagonal from r2