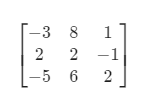Numpy determinant function does not give me the expected output for a 3 by 3 matrix-CodePudding

I just tried to calculate the determinant of the below matrix with numpy np.linalg.det function and I got -4.884981308350685e-15, while chatgpt gave me -41.0.

I tried solving that and I got 36 which indicates that the matrix is non-singular, what am I getting wrong here?

import numpy as np
array = np.array([[-3,8,1],
         [2,2,-1],
        [-5,6,2]],)
determinant = np.linalg.det(array)
print(determinant)

CodePudding user response：

ChatGPT is wrong. And so is your own computation.

Determinant of your matrix is 0.

| -3   8   1 |
|  2   2  -1 | = 
| -5   6   2 |

(add 2×column 3 to column 1) 

| -1   8   1 |
|  0   2  -1 | =
| -1   6   2 |

(add 2×column 3 to column 2)

| -1  10   1 |
|  0   0  -1 | =
| -1  10   2 |

(factorize by -1 and remove line 2 column 3 — so, two -1 factors) 

| -1  10 |
| -1  10 |

= 0 (there are 2 identical lines, so 0)

Numpy is right. Somehow. But, as the "num" in "numpy" indicates, it is numerical computation. So there is a numerical error. Order of magnitude 10⁻¹⁵, not that much (that is about 2⁻⁴⁸, when you have values in the order of magnitude of 2⁴ in the computation. So a numerical error about 2⁵² times smaller that the number involved. Which precisely matches the 52 significant bits of a float64).

If you want to get a real 0, you could use sympy

import sympy
M=sympy.Matrix([[-3, 8, 1], [2,2,-1], [-5,6,2]])
M.det() # 0

Note that even there, it is not miraculous. It works here, and gives an exact 0, because I gave exact values for the matrix. I know they are exact values because they are integers small enough, that have an exact representation. But not all values are exact

For example

M = sympy.Matrix([[0.1, 0.2, 0.3], [0.1, 0.1, 0.2], [1,4,5]])
# That is matrix  [0.1  0.2  0.3]
#                 [0.1  0.1  0.2]
#                 [  1    4    5]
M.det() # -1.38e-17

This times, even with sympy it doesn't work. Result should be 0. Since the 3rd column is a combination of the 2 first (it is the sum of 1st and 2nd column). This times it is not really numerical computation error. The numerical error is in the matrix from the very beginning. There is no exact representation of 0.1, 0.2 or 0.3. This is directly related to the infamous 0.1 0.2==0.3 whose result is False.

But at least, when I trust that my input values are exact, then sympy does an exact computation. (Note that ChatGPT is almost always wrong on substance. ChatGPT is a chatbot. It has good conversational ability. But it is stupid. It just say any stupid thing elegantly. It is faking coherent speech. It is a little bit like what a Star Trek dialog is to real science. Captain Kirk can say "reverse the photonic thrust of the atomic accelerator", it does the trick for a serial dialog; it sounds scientific enough. But it doesn't mean it is consistent. ChatGPT does that. It imitates human discourse like Captain Kirk imitate scientific discourse. The form is ok, the substance is BS.

If the Turing test is defined as the ability to appear human in a conversation, ChatGPT can be said to pass the Turing Test: it imitates very well a human: a human who is having a stroke, but yet a human)