I'm currently reading Algorithm Design with Haskell by Richard Bird & Jeremy Gibbons, the Saddleback search algorithm is given in chapter 4 after binary search, The problem given for motivation is :

given f:N x N -> N is strictly increasing in both arguments, and a value t find all the pairs (x,y) such that f(x,y)=t.

The first definition is given by search f t =[(x,y) | x ← [0..t],y ← [0..t],t == f(x,y)],which searches starting from the origin at the bottom-left corner to the top-right corner, (the indices are increasing from bottom to top and from left to right), then the book proceeds for improvements.

The second definition is given by search f t =[(x,y) | x ← [0..t], y ← [t,t −1..0],t == f(x, y)], The book quotes this definition with

"The first improvement is to start at the top-left rather than the bottom-left corner", then the book continues till it becomes Theta(m n) for a matrix with dimensions n x m.

The final algorithm looks like this

search f t = searchIn (0,t)
 where searchIn (x, y) | x>t ∨ y<0 =[]
 | z<t = searchIn (x 1, y)
 | z == t = (x, y):searchIn (x 1, y−1)
 | z>t = searchIn (x,y−1)
  where z = f(x,y)

Why is it the case? What's wrong with starting from the origin (0,0)?, also why take x-coordinate to be increasing and y-coordinate to be decreasing, or vice versa (I've seen it on leetCode with x decreasing and y increasing), why not take both coordinates in increasing direction?

CodePudding user response：

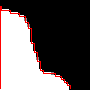
A typical input to the problem will look like this:

The black pixels represent values that are larger than t, the white smaller, and the grey equal. Our goal is to find all the grey spots. Ideally, to do this search, we'd just like to walk along the boundary between black and white. The only problem is we don't know where that boundary starts, so we need to search even to know where to search. If we start at the bottom left, we would have to do something like this:

The first step is to find the boundary, which we can do by scanning up from the bottom left until we find it. But then... we must turn around! The remainder of the search, we proceed down and to the right. So we must separate our search into two phases, one to find the boundary, and another to follow it. If you start in the top left, though...

This time, we don't have to turn around, and this means we can reuse the same code that we use for following the rest of the boundary to find the boundary in the first place!

This answers "why not start at the origin". The other question, "why not increase in one direction and decrease in the other", well... you can. It's an almost identical problem, and an almost identical algorithm will solve it.

CodePudding user response：

I've been reading this and I think I now understand why, in the link, there is a simpler problem about Target sum of two sorted lists,the problem statement :

Given a value k and two sorted lists of integers (all being distinct), find all pairs of integers (i, j) where i j == k.

The solution has to decide which list to move on list1 or list2 or both, and when, it then sorts list1 in ascending order and list2 in descending order, this helps in assigning a decision for each case

let i denote elements list1and j denote elements in list2,

i j < k
i j > k
i j == k

maps to move on (list1, list2, both) respectively.

Now the same applies in the matrix case, assume we start from the origin (0,0), since we traverse each column bottom up, let us be in column a, assume we hit an element z at row b such that z=f(a,b) >= t then we can leave column a and row b, actually the whole upper rectangle having (a,b) as bottom-left corner (since f is strictly increasing in both arguments, and both, starting from the origin, are increasing).

The next starting point will be (a 1,0), but when z=f(a,b) < t we can do nothing, just complete in the current column until we hit an element that is greater than t, or then column ends.

From the search algorithm implementation in the question, it seems that choosing one index to be increasing and the other to be decreasing, introduces more regularity in the implementation, also the new starting points are usually inside the matrix, so we are not doing linear search for points that would reduce the search space, unlike starting from (a 1,0).

I'm not able to do full analysis to see how time complexity is affected in worst case, but I think this is convincing.

Any comments are welcomed, full analysis solutions are greatly appreciated.