How to properly fit a non-linear equation to a set of datapoints?-CodePudding

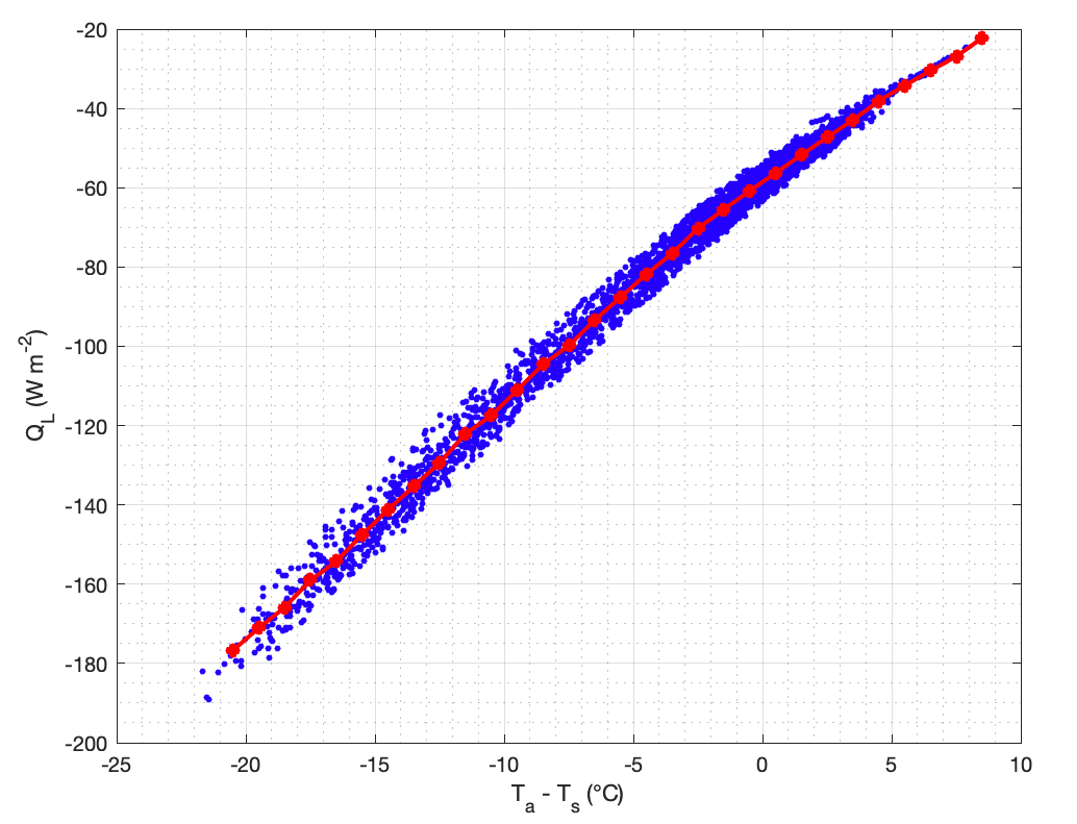
I have a curve of net longwave radiation (QL) data, which are calculated as follows:

QL = a*Ta^4 - b*Ts^4
where a and b are constants, Ta is the air temperature and Ts is the surface temperature

If I plot a curve of QL versus Ta-Ts, what type of equation should I use to fit the data as follows y = f(x) where x = (Ta-Ts)?

Thanks

-20.5   -176.683672
-19.5   -171.0655836
-18.5   -165.8706233
-17.5   -158.9990897
-16.5   -154.2715535
-15.5   -147.5376901
-14.5   -141.2410818
-13.5   -135.3387669
-12.5   -129.3971791
-11.5   -122.0777208
-10.5   -117.475907
-9.5    -111.107148
-8.5    -104.5999237
-7.5    -99.82769298
-6.5    -93.43215832
-5.5    -87.6278432
-4.5    -81.85415752
-3.5    -76.5997892
-2.5    -70.26308516
-1.5    -65.49437303
-0.5    -60.78052134
0.5 -56.32077454
1.5 -51.74037492
2.5 -47.30542394
3.5 -42.92298839
4.5 -38.13260904
5.5 -34.22676827
6.5 -30.49502686
7.5 -26.89383663
8.5 -22.259631

The complete data

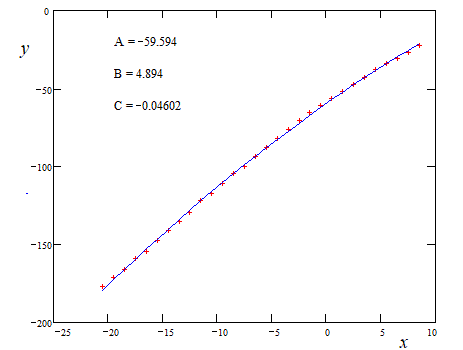
The coefficients A,B,C are purely mathematical without physical signifiance. The coefficients a and b in f(x)=aTa^4 bTs^4 cannot be derived from the coefficients A,B,C without more physical information as already pointed out.

CodePudding user response：

I took your data and did a 4th order polynomial fit. Here's the result:

QL = -58.607   x*(4.8336   x*(-0.0772   x*(-2e-5   x*8e-5)))

R^ = 0.9999

x = (Ta - Ts)

If you want the equation to be in terms of Ta and Ts instead of the difference you should substitute and do the algebra.