In programming, I used only Integers. But this time for some calculations. I need to calculate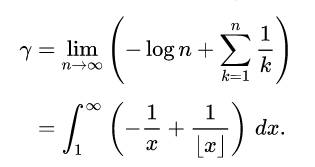

• [x] = gif(x) = math.ceil(x)

But, I doubt the precision Numerical Algorithm

I need higher degree of accuracy using Python.

CodePudding user response：

From the French Wikipedia discussion page, an approximation to 6 decimal places:

import math as m
EulerMascheroniApp = round( (1.-m.gamma(1 1.e-8))*1.e14 )*1.e-6
print(EulerMascheroniApp)
# 0.577216 

This constant is also available in the sympy module, under the name EulerGamma:

>>> import sympy
>>> sympy.EulerGamma
EulerGamma
>>> sympy.EulerGamma.evalf()
0.577215664901533
>>> - sympy.polygamma(0,1)
EulerGamma
>>> sympy.stieltjes(0)
EulerGamma
>>> sympy.stieltjes(0, 1)
EulerGamma

Documentation:

• math.gamma;
• sympy.EulerGamma;
• sympy.functions.special;
• sympy: numerical evaluation.

On this last documentation link, you can find more information about how to evaluate the constant with more precision, if the default of .evalf() is not enough.

If you still want to compute the constant yourself as an exercise, I suggest comparing your results to sympy's constant, to check for accuracy and correctness.

CodePudding user response：

You can calculate it using python Decimal built-in module to control how many decimals (https://docs.python.org/2/library/decimal.html) you are going to use.

a = 1/7
len(str(a))-2
Out[1] 17

using Decimal:

from decimal import *
getcontext().prec = 90 #90 decimals precision
a = Decimal(1) / Decimal(7)
len(str(a))-2
Out[2] 90

basically:

n = 100000
Euler_Mascheroni = -Decimal(log(Decimal(n)))   sum([Decimal(1)/Decimal(i) for i in range(1,n)])
Euler_Mascheroni

Out[3] 0.5772106648931993300735700990829054997103249183447011016275294159381819822823091944316360