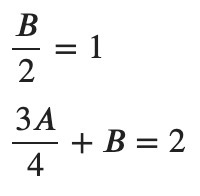How to match real numeric coefficients for two expression in Sympy-CodePudding

If you look at this example: 2Bsin(x) (B ¾A)*cos(x) = sin(x) 2cos(x) it’s easy to see that 2B = 1, B ¾A = 2 and applying some basic linear algebra B = ½, A = 2 In Python, using sympy, however, you run this code:

from sympy import *; var('x A B')

P1 = (B/2)*sin(x)   (B   3*A/4)*cos(x)
P2 = sin(x)   2*cos(x)
solve(Eq(P1, P2), [A,B])

you get this

[(-2*B*tan(x)/3 - 4*B/3   4*tan(x)/3   4/3, B)]

Is there a way to get the result in terms of A and B?

CodePudding user response：

It seems like a little bit of a hack but works. I substitute sin(x) and cos(x) by x and y and turn it into a polynomial. Then I can just get the coefficients, make an equation out of those and solve it just fine.

from sympy import *; var('x y A B')

P1 = (B/2)*sin(x)   (B   3*A/4)*cos(x)
P2 = sin(x)   2*cos(x)
P1s = P1.subs({sin(x):x, cos(x):y})
P2s = P2.subs({sin(x):x, cos(x):y})

eqs = tuple(map(lambda x:Eq(*x),zip(Poly(P1s,[x,y]).coeffs(), Poly(P2s,[x,y]).coeffs())))

Those sympy does solve

sol = solve(eqs)

{A: 0, B: 2}

And I can even put those into the original equation to see if something weird happened:

P1.subs(sol), P2.subs(sol)

(sin(x)   2*cos(x), sin(x)   2*cos(x))