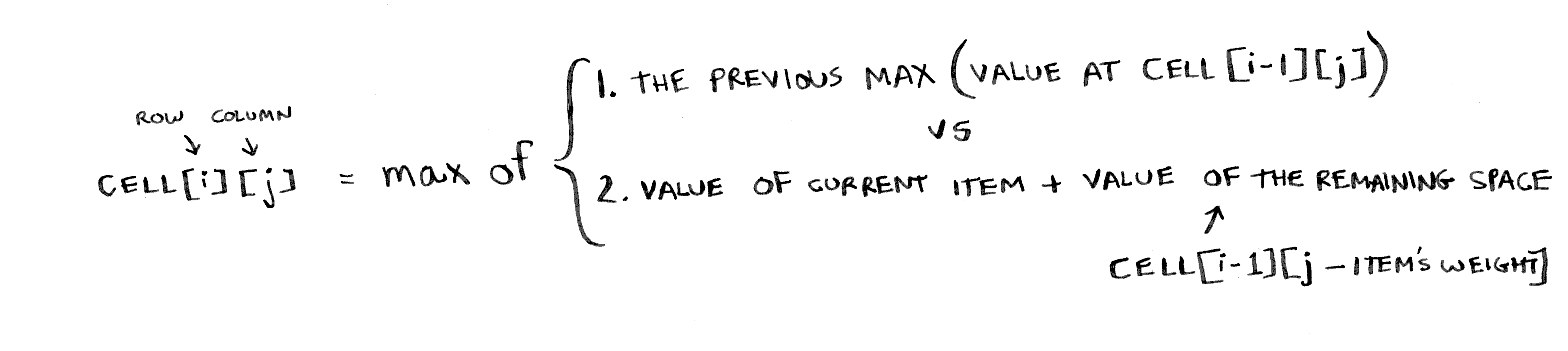Confusing Output for 0/1 Knapsack Problem-CodePudding

I'm learning Dynamic Programming, and have the book

When I run the code below, which is supposed to implement the 0/1 Knapsack Problem in Python, I get the following output:

 --- ------ ------ ------ ------ 
| 0 |  0   |  0   |  0   |  0   |
| 0 | 1500 | 1500 | 1500 | 1500 |
| 0 | 1500 | 1500 | 2000 | 3500 |
| 0 | 1500 | 1500 | 2000 | 3500 |
 --- ------ ------ ------ ------ 
3500

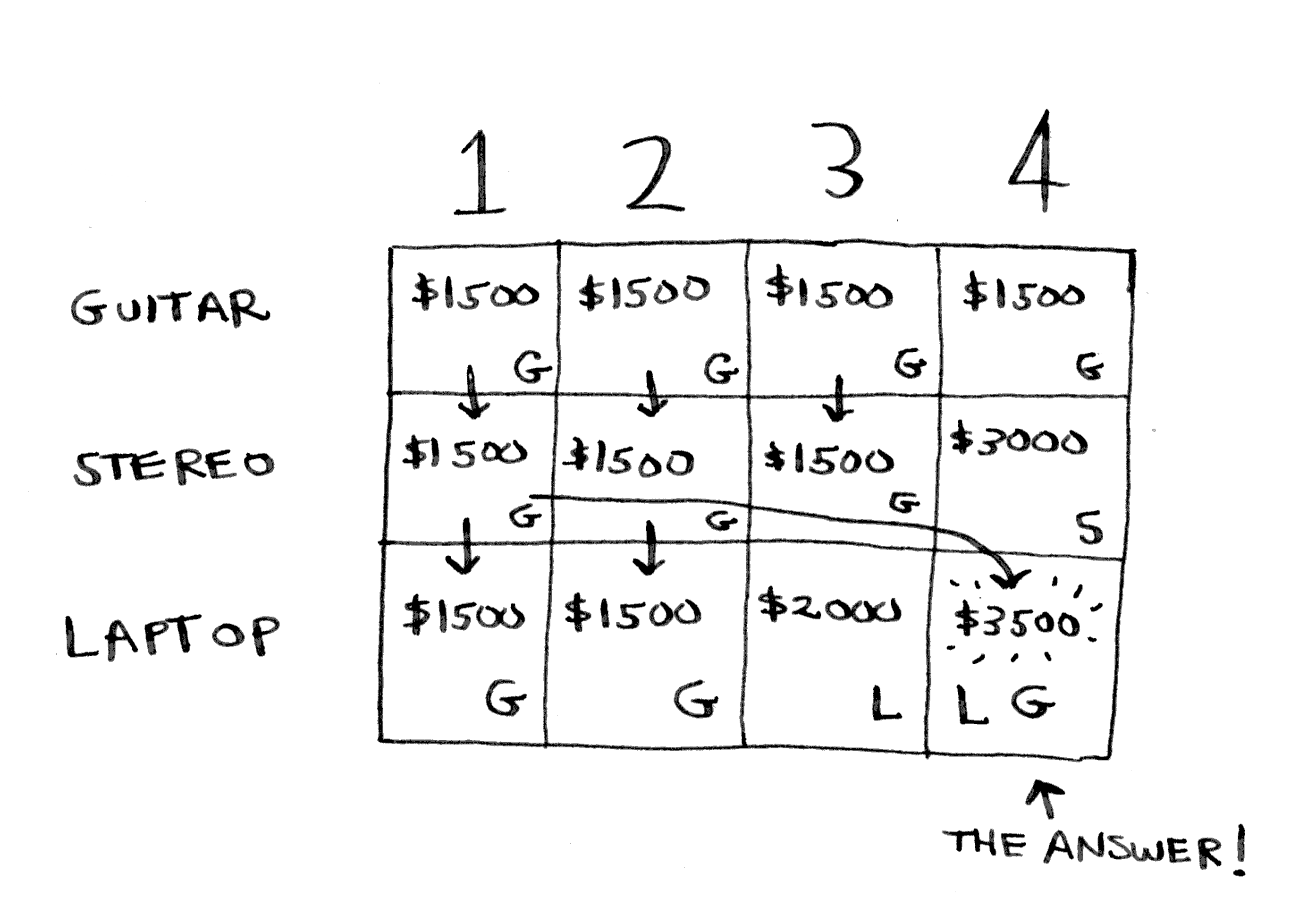
The solution is correct, but it looks like this is a coincidence, as the table generated by the code is different from that given in the image from the book.

Could someone please explain why the table generated by the code is different from the one in the book?

Could it be that the formula used to generate the table is different (as in different in effect - I can see that they are not identical)? The one in the book is:

# A Dynamic Programming based Python
# Program for 0-1 Knapsack problem
# Returns the maximum value that can
# be put in a knapsack of capacity W
from tabulate import tabulate


def knapSack(W, wt, val, n):
    K = [[0 for x in range(W   1)] for x in range(n   1)]

    # Build table K[][] in bottom up manner
    for i in range(n   1):
        for w in range(W   1):
            if i == 0 or w == 0:
                K[i][w] = 0
            elif wt[i - 1] <= w:
                K[i][w] = max(val[i - 1]
                                K[i - 1][w - wt[i - 1]],
                              K[i - 1][w])
            else:
                K[i][w] = K[i - 1][w]
    print(tabulate(K, tablefmt="pretty"))

    return K[n][W]


# Driver code
val = [1500, 2000, 3000]
wt = [1, 3, 4]
W = 4
n = len(val)
print(knapSack(W, wt, val, n))

CodePudding user response：

 --- ------ ------ ------ ------ 
| 0 |  0   |  0   |  0   |  0   |
| 0 | 1500 | 1500 | 1500 | 1500 |  guitar
| 0 | 1500 | 1500 | 2000 | 3500 |  laptop
| 0 | 1500 | 1500 | 2000 | 3500 |  stereo
 --- ------ ------ ------ ------ 
3500

Your listing is [guitar, laptop, stereo], however in the solution of the author, listing is [guitar, stereo, laptop]. That's why your tables are different and that's all. Your solution is indeed correct. Try to run your solution with the listing of the author:

from tabulate import tabulate

def knapSack(W, wt, val, n):
    K = [[0 for x in range(W   1)] for x in range(n   1)]

    # Build table K[][] in bottom up manner
    for i in range(n   1):
        for w in range(W   1):
            if i == 0 or w == 0:
                K[i][w] = 0
            elif wt[i - 1] <= w:
                K[i][w] = max(val[i - 1]
                                K[i - 1][w - wt[i - 1]],
                              K[i - 1][w])
            else:
                K[i][w] = K[i - 1][w]
    print(tabulate(K, tablefmt="pretty"))

    return K[n][W]


# Driver code
val = [1500, 3000, 2000]
wt = [1, 4, 3]
W = 4
n = len(val)
print(knapSack(W, wt, val, n))

Output:

 --- ------ ------ ------ ------ 
| 0 |  0   |  0   |  0   |  0   |
| 0 | 1500 | 1500 | 1500 | 1500 |   guitar
| 0 | 1500 | 1500 | 1500 | 3000 |   stereo
| 0 | 1500 | 1500 | 2000 | 3500 |   laptop
 --- ------ ------ ------ ------ 
3500