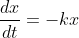Discrepancy in curve fit using solutions from solve

Here's a basic example equation that I am trying to fit to an example data.

The goal is to find the best fit of k for my data assuming the data follows the above equation. An obvious way to do so is to numerically integrate the equation and then use curve fitting methods to minimise the least squares and get k.

Numerically integrating using

## SciPy, NumPy etc imports here

N_SAMPLES = 20
rnd = np.random.default_rng(12345)
times = np.sort(rnd.choice(rnd.uniform(0, 1, 100), N_SAMPLES))
vals = np.logspace(10, 0.1, N_SAMPLES)   rnd.uniform(0, 1, N_SAMPLES)


def using_ivp(t, k):
    eqn = lambda t, x, k: -k * x
    y0 = vals[0]
    sol = solve_ivp(eqn, t, y0=[y0], args=(k, ),
                    dense_output=True)
    return sol.sol(t)[0]

def using_odeint(t, k):
    eqn = lambda x, t: -k * x
    y0 = vals[0]
    sol = odeint(eqn, y0, t)
    return sol[:,0]
    
tfit = np.linspace(min(times), max(times), 100)


#Fitting using ivp
k_fit1, kcov1 = curve_fit(using_ivp, times, vals, p0=1.3)
fit1 = using_ivp(tfit, k_fit1)


#Fitting using odeint
k_fit2, kcov2 = curve_fit(using_odeint, times, vals, p0=1.3)
fit2 = using_odeint(tfit, k_fit2)

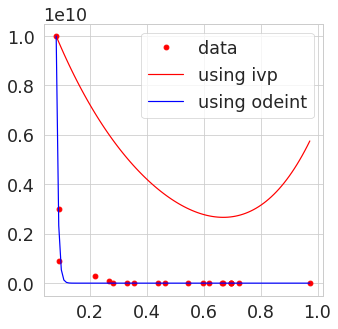
plt.figure(figsize=(5, 5))
plt.plot(times, vals, 'ro', label='data')
plt.plot(tfit, fit1, 'r-', label='using ivp')
plt.plot(tfit, fit2, 'b-', label='using odeint')
plt.legend(loc='best');

print('Best fit k using ivp = {}\n'\
      'Best fit k using odeint = {}\n'.\
      format(k_fit1, k_fit2))

CodePudding user response：

Check again what the input arguments of solve_ivp are. The integration interval is given by the first two numbers in the t_span argument, so in your application most values in sol.sol(t) are obtained via wild extrapolation.

Correct that by giving the interval as [min(t),max(t)].

To get more compatible computations, explicitly set the error tolerances, as the default values need not be equal. For instance atol=1e-22, rtol=1e-9 so that only the relative tolerance has an effect.

It is curious how you use the args mechanism. It was only recently introduced to solve_ivp to be more compatible with odeint. I would not use it in either case here, as the definition of the parameter and its use is contained in a 3-line block. It has its uses where proper encapsulation and isolation from other code is a real concern.