I am solving this question on LeetCode.com called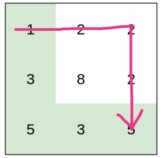

The code I have is:

class Solution {
public:
    vector<pair<int,int>> getNeighbors(vector<vector<int>>& h, int r, int c) {
        vector<pair<int,int>> n;
        if(r 1<h.size()) n.push_back({r 1,c});
        if(c 1<h[0].size()) n.push_back({r,c 1});
        if(r-1>=0) n.push_back({r-1,c});
        if(c-1>=0) n.push_back({r,c-1});
        return n;
    }
    
    int minimumEffortPath(vector<vector<int>>& heights) {
        int rows=heights.size(), cols=heights[0].size();
        
        using arr=array<int, 3>;
        priority_queue<arr, vector<arr>, greater<arr>> pq;
        vector<vector<int>> dist(rows, vector<int>(cols, INT_MAX));
        pq.push({0,0,0});    //r,c,weight
        dist[0][0]=0;
        
        //Dijkstra
        while(pq.size()) {
            auto [r,c,wt]=pq.top();
            pq.pop();
            
            if(wt>dist[r][c]) continue;
            
            vector<pair<int,int>> neighbors=getNeighbors(heights, r, c);
            for(auto n: neighbors) {
                int u=n.first, v=n.second;
                int curr_cost=abs(heights[u][v]-heights[r][c]);
                if(dist[u][v]>max(curr_cost,wt)) {
                    dist[u][v]=max(curr_cost,wt);
                    pq.push({u,v,dist[u][v]});
                }
            }
        }
        
        return dist[rows-1][cols-1];
    }
};

This gets accepted, but I have two questions:

a. Since we update dist[u][v] if it is greater than max(curr_cost,wt), how does it guarantee that in the end we return the minimum effort required? That is, why don't we end up returning the effort of the one in red above?

b. Some solutions such as this one, short-circuit and return immediately when we reach the bottom right the first time (ie, if(r==rows-1 and c==cols-1) return wt;) - how does this work? Can't we possibly get a shorter dist when we revisit the bottom right node in future?

CodePudding user response：

The problem statement requires that we find the path with the minimum "effort".
And "effort" is defined as the maximum difference in heights between adjacent cells on a path.

The expression max(curr_cost, wt) takes care of the maximum part of the problem statement. When moving from one cell to another, the distance to the new cell is either the same as the distance to the old cell, or it's the difference in heights, whichever is greater. Hence max(difference_in_heights, distance_to_old_cell).

And Dijkstra's algorithm takes care of the minimum part of the problem statement, where instead of using a distance from the start node, we're using the "effort" needed to get from the start node to any given node. Dijkstra's attempts to minimize the distance, and hence it minimizes the effort.

Dijkstra's has two closely related concepts: visited and explored. A node is visited when any incoming edge is used to arrive at the node. A node is explored when its outgoing edges are used to visit its neighbors. The key design feature of Dijkstra's is that after a node has been explored, additional visits to that node will never improve the distance to that node. That's the reason for the priority queue. The priority queue guarantees that the node being explored has the smallest distance of any unexplored nodes.

In the sample grid, the red path will be explored before the green path because the red path has effort 1 until the last move, whereas the green path has effort 2. So the red path will set the distance to the bottom right cell to 3, i.e. dist[2][2] = 3.

But when the green path is explored, and we arrive at the 3 at row=2, col=1, we have

• dist[2][2] = 3
• curr_cost=2
• wt=2

So dist[2][2] > max(curr_cost, wt), and dist[2][2] gets reduced to 2.

The answers to the questions:

a. The red path does set the bottom right cell to a distance of 3, temporarily. But the result of the red path is discarded in favor of the result from the green path. This is the natural result of Dijkstra's algorithm searching for the minimum.

b. When the bottom right node is ready to be explored, i.e. it's at the head of the priority queue, then it has the best distance it will ever have, so the algorithm can stop at that point. This is also a natural result of Dijkstra's algorithm. The priority queue guarantees that after a node has been explored, no later visit to that node will reduce its distance.