I've a set of data and I want to fit these data to a damped cosine function i.e. "A*.cos(K*x).exp(-Bx)". To do this, I've used the following code, but the fitting is very bad. Can anyone suggest me to find the best fit? x & y data are the following:
x=[1.3, 1.7, 1.72, 1.84, 1.98, 2.02, 2.16, 2.2, 2.2, 2.3, 2.38, 2.5, 2.55, 2.75, 2.8, 2.82, 2.84, 2.9, 2.92, 3.1, 3.13, 3.18, 3.19, 3.22, 3.3, 3.38, 3.44, 3.49, 3.62, 3.64, 3.72, 3.72, 3.75, 3.8, 3.82, 3.86, 3.92, 4.0, 4.07, 4.1, 4.1, 4.13, 4.14, 4.14, 4.17, 4.21, 4.24, 4.24, 4.24, 4.28, 4.3, 4.38, 4.49, 4.62, 4.62, 4.67, 4.72, 4.73, 4.74, 4.76, 4.76, 4.81, 4.81, 4.88, 4.89, 4.9, 4.9, 4.94, 4.96, 5.03, 5.05, 5.06, 5.1, 5.1, 5.15, 5.16, 5.16, 5.19, 5.22, 5.22, 5.3, 5.37, 5.41, 5.46, 5.56, 5.63, 5.65, 5.65, 5.73, 5.76, 5.81, 5.86, 5.91, 5.98, 6.03, 6.05, 6.05, 6.06, 6.11, 6.14, 6.22, 6.25, 6.27, 6.27, 6.3, 6.3, 6.31, 6.36, 6.42, 6.42, 6.47, 6.48, 6.5, 6.51, 6.58, 6.59, 6.62, 6.65, 6.66, 6.67, 6.69, 6.72, 6.77, 6.8, 6.84, 6.87, 6.91, 6.94, 6.94, 6.94, 7.05, 7.14, 7.17, 7.22, 7.23, 7.24, 7.32, 7.32, 7.35, 7.38, 7.4, 7.41, 7.42, 7.44, 7.45, 7.49, 7.5, 7.52, 7.54, 7.6, 7.72, 7.75, 7.81, 7.9, 7.92, 7.95, 7.97, 7.98, 7.99, 8.02, 8.03, 8.03, 8.05, 8.06, 8.07, 8.1, 8.12, 8.14, 8.19, 8.2, 8.21, 8.24, 8.25, 8.28, 8.28, 8.29, 8.32, 8.38, 8.38, 8.43, 8.49, 8.52, 8.54, 8.54, 8.57, 8.7, 8.75, 8.75, 8.78, 8.79, 8.88, 8.88, 8.93, 8.95, 9.0, 9.01, 9.02, 9.03, 9.06, 9.07, 9.11, 9.14, 9.16, 9.17, 9.18, 9.19, 9.2, 9.3, 9.33, 9.44, 9.46, 9.59, 9.62, 9.62, 9.64, 9.66, 9.71, 9.73, 9.73, 9.75, 9.76, 9.76, 9.79, 9.88, 9.9, 9.93, 9.93, 9.95, 9.99, 10.01, 10.03, 10.04, 10.05, 10.07, 10.11, 10.13, 10.18, 10.22, 10.22, 10.31, 10.37, 10.38, 10.41, 10.42, 10.44, 10.5, 10.52, 10.55, 10.56, 10.56, 10.58, 10.6, 10.66, 10.68, 10.68, 10.69, 10.7, 10.73, 10.75, 10.81, 10.93, 10.96, 10.98, 10.98, 11.02, 11.04, 11.1, 11.14, 11.15, 11.15, 11.17, 11.19, 11.21, 11.23, 11.24, 11.28, 11.3, 11.31, 11.32, 11.33, 11.4, 11.42, 11.48, 11.5, 11.51, 11.6, 11.62, 11.62, 11.63, 11.65, 11.72, 11.74, 11.74, 11.94, 11.95, 11.98, 12.02, 12.02, 12.03, 12.04, 12.09, 12.11, 12.17, 12.2, 12.23, 12.26, 12.3, 12.31, 12.33, 12.33, 12.37, 12.38, 12.61, 12.63, 12.69, 12.7, 12.74, 12.79, 12.8, 12.84, 12.87, 12.9, 12.91, 12.92, 12.94, 13.0, 13.19, 13.2, 13.26, 13.29, 13.3, 13.31, 13.31, 13.34, 13.35, 13.36, 13.44, 13.48, 13.52, 13.59, 13.78, 13.83, 13.88, 13.98, 14.02, 14.05, 14.07, 14.1, 14.14, 14.19, 14.25, 14.33, 14.36, 14.38, 14.41, 14.46, 14.47, 14.53, 14.54, 14.57, 14.69, 14.72, 14.77, 14.78, 14.78, 14.8, 14.82, 14.82, 14.91, 14.92, 14.96, 14.96, 15.05, 15.09, 15.17, 15.2, 15.21, 15.25, 15.26, 15.31, 15.32, 15.36, 15.36, 15.4, 15.4, 15.4, 15.41, 15.47, 15.52, 15.6, 15.61, 15.61, 15.63, 15.65, 15.71, 15.77, 15.8, 15.84, 15.86, 15.88, 15.94, 15.94, 15.97, 15.98, 16.02, 16.03, 16.27, 16.43, 16.56, 16.64, 16.64, 16.64, 16.68, 16.88, 16.91, 16.92, 16.93, 16.97, 16.99, 17.0, 17.01, 17.02, 17.05, 17.13, 17.21, 17.32, 17.45, 17.59, 17.79, 17.8, 17.81, 17.87, 17.9, 17.92, 17.93, 17.93, 17.97, 17.98, 18.02, 18.05, 18.08, 18.11, 18.2, 18.24, 18.4, 18.48, 18.5, 18.51, 18.59, 18.65, 18.76, 18.76, 18.86, 18.86, 18.86, 18.87, 18.9, 18.92, 18.93, 19.05, 19.06, 19.17, 19.26, 19.27, 19.41, 19.47, 19.48, 19.54, 19.6, 19.66, 19.67, 19.68, 19.8, 19.9, 20.01, 20.04, 20.1, 20.49, 20.49, 20.5, 20.56, 20.65, 20.65, 20.7, 20.71, 20.78, 20.91, 21.11, 21.19, 21.2, 21.28, 21.29, 21.58, 21.62, 21.7, 21.7, 21.76, 21.76, 21.84, 21.85, 21.87, 21.9, 21.94, 22.0, 22.02, 22.09, 22.16, 22.3, 22.3, 22.41, 22.51, 22.53, 22.71, 22.77, 22.94, 23.17, 23.25, 23.33, 23.72, 23.87, 24.12, 24.14, 24.19, 24.34, 24.4, 24.6, 24.62, 24.62, 24.8, 25.01, 25.13, 25.4, 25.42, 25.81, 25.85, 25.89, 26.03, 26.17, 26.22, 26.41, 26.98, 27.01, 27.02, 27.06, 27.17, 27.49, 27.73, 28.14, 28.23, 28.37, 28.56, 28.83, 28.84, 30.32, 30.57, 31.95, 33.23, 33.46, 33.81, 33.85, 34.44]
y=[0.97119140625, 0.7978515625, 0.88525390625, 0.87255859375, 0.9228515625, 0.9677734375, 0.931640625, 0.953125, 0.96484375, 0.67041015625, 0.685546875, 0.8740234375, 0.82958984375, 0.79736328125, 0.8046875, 0.87841796875, 0.62109375, 0.5986328125, 0.826171875, 0.57470703125, 0.921875, 0.51025390625, 0.87939453125, 0.79638671875, 0.76513671875, 0.6318359375, 0.80126953125, 0.58447265625, 0.7392578125, 0.7802734375, 0.5703125, 0.77587890625, 0.6748046875, 0.826171875, 0.88671875, 0.85986328125, 0.80078125, 0.7099609375, 0.6474609375, 0.5439453125, 0.7001953125, 0.8896484375, 0.87744140625, 0.9306640625, 0.7021484375, 0.8603515625, 0.302490234375, 0.66552734375, 0.75390625, 0.71240234375, 0.52392578125, 0.8662109375, 0.66650390625, 0.35986328125, 0.46044921875, 0.58984375, 0.7548828125, 0.80322265625, 0.8193359375, 0.27880859375, 0.638671875, 0.53466796875, 0.65625, 0.302734375, 0.429443359375, 0.251708984375, 0.6982421875, 0.7626953125, 0.65966796875, 0.62451171875, 0.47998046875, 0.65087890625, -0.0224456787109375, 0.748046875, 0.70458984375, 0.43603515625, 0.53369140625, 0.391845703125, 0.4921875, 0.75830078125, 0.828125, 0.4521484375, 0.701171875, 0.83251953125, 0.55908203125, 0.80078125, 0.297119140625, 0.54150390625, 0.374755859375, 0.60205078125, 0.66064453125, 0.412353515625, 0.30615234375, 0.2486572265625, 0.432861328125, 0.1175537109375, 0.70849609375, -0.20458984375, 0.5771484375, 0.254638671875, 0.68359375, -0.05792236328125, 0.34033203125, 0.37060546875, 0.56982421875, 0.8056640625, 0.09881591796875, 0.65625, 0.23388671875, 0.491455078125, 0.331787109375, 0.1302490234375, 0.791015625, 0.5986328125, 0.399658203125, 0.61376953125, 0.53076171875, 0.210693359375, 0.4423828125, 0.5751953125, 0.495361328125, 0.2384033203125, 0.7333984375, 0.39111328125, 0.1533203125, 0.4951171875, 0.28515625, 0.048065185546875, 0.345947265625, 0.3798828125, -0.0243988037109375, 0.576171875, 0.2127685546875, 0.417724609375, 0.408447265625, 0.5673828125, 0.1680908203125, 0.58203125, 0.6337890625, 0.1171875, 0.59814453125, 0.321044921875, 0.133056640625, 0.2437744140625, 0.005306243896484375, 0.1336669921875, -0.5703125, 0.5693359375, 0.418701171875, 0.1077880859375, -0.1431884765625, 0.51220703125, 0.0021724700927734375, 0.1805419921875, 0.5546875, 0.35107421875, 0.17919921875, 0.2413330078125, 0.1287841796875, 0.032440185546875, 0.435546875, 0.5166015625, 0.227783203125, 0.478271484375, 0.11627197265625, 0.384033203125, 0.54541015625, 0.008514404296875, 0.1456298828125, 0.2265625, 0.6953125, 0.5576171875, 0.471435546875, 0.146240234375, 0.673828125, 0.1785888671875, 0.278564453125, 0.03521728515625, 0.197021484375, 0.4091796875, 0.2105712890625, 0.6767578125, 0.292236328125, 0.61669921875, 0.5078125, 0.48486328125, -0.05682373046875, 0.3623046875, 0.441162109375, 0.0307769775390625, 0.10516357421875, 0.4541015625, 0.53076171875, -0.0219879150390625, 0.59423828125, 0.07867431640625, 0.383544921875, 0.64111328125, -0.038848876953125, -0.1036376953125, 0.0213470458984375, -0.0007333755493164062, 0.556640625, 0.462158203125, 0.470458984375, 0.305908203125, 0.436767578125, 0.1883544921875, 0.07977294921875, 0.54150390625, -0.11492919921875, 0.043975830078125, 0.07244873046875, 0.1573486328125, 0.141357421875, 0.52294921875, 0.10198974609375, -0.13916015625, 0.2314453125, 0.1143798828125, 0.1435546875, 0.361083984375, 0.2822265625, 0.6767578125, 0.272216796875, 0.035369873046875, 0.54638671875, 0.35986328125, 0.1324462890625, 0.283935546875, -0.359375, 0.113525390625, 0.444580078125, 0.08453369140625, -0.0662841796875, 0.60302734375, -0.058258056640625, 0.2232666015625, 0.572265625, 0.1064453125, 0.234130859375, 0.316650390625, 0.5888671875, 0.034881591796875, 0.038330078125, 0.09259033203125, 0.387939453125, 0.31640625, 0.09906005859375, 0.295654296875, 0.06787109375, 0.2222900390625, 0.51318359375, -0.2303466796875, 0.08935546875, 0.01538848876953125, 0.301513671875, -0.0555419921875, 0.167236328125, 0.348388671875, 0.259033203125, -0.12115478515625, 0.21875, 0.2255859375, -0.007389068603515625, 0.352783203125, 0.280517578125, 0.477294921875, 0.0997314453125, 0.241455078125, 0.207763671875, 0.485107421875, -0.04827880859375, -0.1048583984375, 0.301025390625, 0.333984375, 0.17041015625, 0.16552734375, 0.533203125, 0.25439453125, 0.1949462890625, -0.0609130859375, 0.1912841796875, 0.149658203125, -0.01195526123046875, 0.100830078125, -0.150390625, 0.134765625, 0.2003173828125, 0.323974609375, 0.2391357421875, 0.0166473388671875, 0.54443359375, 0.2197265625, 0.270751953125, 0.07989501953125, 0.01105499267578125, 0.1248779296875, 0.1544189453125, 0.462646484375, -0.322021484375, 0.18017578125, 0.474609375, 0.485595703125, 0.0941162109375, -0.08319091796875, 0.08697509765625, 0.10546875, 0.1292724609375, 0.50830078125, 0.395751953125, 0.0179290771484375, 0.0831298828125, 0.406982421875, 0.2496337890625, 0.2181396484375, -0.3525390625, -0.225341796875, 0.072265625, 0.420654296875, 0.24072265625, 0.020782470703125, 0.02197265625, -0.09930419921875, 0.080810546875, -0.0816650390625, 0.444580078125, -0.052215576171875, 0.107666015625, 0.466552734375, 0.33935546875, 0.23974609375, 0.384033203125, 0.301025390625, 0.1275634765625, -0.253173828125, -0.2286376953125, -0.0204925537109375, 0.1527099609375, 0.256103515625, 0.09405517578125, 0.2166748046875, 0.0221710205078125, 0.1700439453125, 0.1451416015625, -0.09765625, 0.1456298828125, 0.26708984375, 0.045654296875, -0.007354736328125, -0.037353515625, 0.1895751953125, 0.55615234375, 0.039764404296875, 0.12432861328125, 0.335205078125, 0.66943359375, 0.373779296875, 0.37646484375, -0.2939453125, 0.261474609375, 0.24365234375, -0.19384765625, -0.072265625, 0.2213134765625, 0.09710693359375, 0.302734375, 0.383544921875, 0.48193359375, 0.308837890625, 0.058074951171875, 0.42431640625, 0.21142578125, 0.033294677734375, 0.22265625, 0.26953125, -0.027435302734375, 0.42529296875, 0.1778564453125, 0.1683349609375, 0.52734375, 0.0005445480346679688, 0.11578369140625, -0.1346435546875, 0.19384765625, 0.331298828125, 0.349609375, 0.376953125, 0.333984375, 0.28466796875, 0.0650634765625, 0.1923828125, -0.2154541015625, 0.361572265625, 0.44580078125, 0.44287109375, 0.04351806640625, -0.2607421875, 0.5419921875, 0.271240234375, 0.114501953125, 0.375, 0.306884765625, -0.2227783203125, 0.3466796875, 0.137939453125, 0.193115234375, 0.311767578125, -0.0274810791015625, 0.0167694091796875, 0.35595703125, 0.54736328125, -0.058563232421875, 0.0077056884765625, -0.2330322265625, 0.326171875, 0.0859375, -0.235595703125, 0.197021484375, 0.5576171875, 0.51611328125, 0.40087890625, 0.35986328125, 0.01483154296875, -0.077392578125, 0.277587890625, 0.12103271484375, 0.384521484375, 0.59765625, 0.353515625, 0.44091796875, 0.0006513595581054688, -0.01324462890625, 0.30029296875, 0.310302734375, 0.382080078125, 0.27099609375, 0.291015625, -0.158447265625, 0.11834716796875, 0.1761474609375, 0.2432861328125, 0.00070953369140625, 0.406494140625, 0.294921875, 0.03253173828125, 0.46337890625, 0.27294921875, 0.342041015625, 0.08038330078125, -0.11114501953125, 0.312744140625, 0.3662109375, 0.42626953125, 0.452392578125, 0.5439453125, 0.4130859375, -0.21728515625, 0.352783203125, -0.037506103515625, 0.341064453125, 0.4248046875, 0.306640625, -0.012786865234375, 0.042449951171875, 0.272216796875, 0.3134765625, 0.16455078125, 0.54052734375, 0.447021484375, 0.0677490234375, 0.401123046875, 0.290771484375, 0.12176513671875, -0.059112548828125, -0.151123046875, 0.1878662109375, -0.07684326171875, 0.01140594482421875, 0.481201171875, 0.2120361328125, 0.1907958984375, 0.29248046875, 0.050689697265625, 0.308837890625, 0.371337890625, 0.1312255859375, 0.34765625, 0.298583984375, 0.446044921875, -0.2298583984375, 0.171875, -0.184814453125, 0.5068359375, 0.310546875, 0.324462890625, 0.25, 0.53076171875, 0.5400390625, 0.231689453125, 0.671875, -0.1876220703125, 0.412109375, 0.5546875, 0.049224853515625, 0.2388916015625, 0.5869140625, 0.11663818359375, 0.61767578125, 0.31591796875, 0.297119140625, 0.107666015625, 0.56005859375, 0.129638671875, -0.278564453125, 0.279052734375, 0.0285491943359375, 0.5712890625, -0.212646484375, -0.2064208984375, -0.11956787109375, -0.2783203125, -0.421630859375, -0.194580078125, 0.4541015625, 0.51171875, 0.208740234375, 0.395263671875, -0.252197265625, -0.17578125, -0.322509765625, 0.5654296875, 0.4208984375, -0.412353515625, 0.1898193359375, 0.193603515625, 0.541015625, 0.065185546875, 0.6015625, 0.21923828125, -0.06341552734375, 0.390380859375, -0.31201171875, 0.58251953125, 0.307373046875, 0.056610107421875, -0.140869140625, -0.0220184326171875, -0.07080078125, -0.26220703125, -0.313232421875, 0.439208984375, 0.38427734375, -0.18603515625, -0.095458984375, 0.164306640625, -0.12548828125, -0.1468505859375, 0.1876220703125, 0.2489013671875, -0.14013671875]
from scipy.optimize import curve_fit
import numpy as np
x = np.array(x)
y = np.array(y)
def fit_cosine(x, y):
guess_amp = 1 # A
guess_wave_no = .05# K
guess_dampcoeff = 0 # B
guess = np.array([guess_amp, guess_wave_no, guess_dampcoeff])
def cos_func(x, A, K, B): return A * np.cos(K*x)*np.exp(-1*B*x)
popt, pcov = curve_fit(cos_func, x, y, p0=guess, maxfev=5000)
A, K, B = popt
fitfunc = lambda x: A * np.cos(K*x)* np.exp(-1*B*x)
return {"amp": A, "omega": K, "decay": B, "fitfunc": fitfunc, "maxcov": np.max(pcov), "rawres": (guess, popt, pcov)}
import matplotlib.pyplot as plt
res = fit_cosine(x, y)
print("Amplitude=%(amp)s, WaveNumber =%(omega)s, DampingCoefficient = %(decay)s, Max. Cov.=%(maxcov)s" % res)
plt.figure()
plt.scatter(x, y, label="Coherence")
#plt.plot(x, res["fitfunc"](x), "r-", label="y fit curve", linewidth=2)
plt.legend(loc="best")
plt.show()
CodePudding user response:
The fitting is difficult due to the high level of scatter.
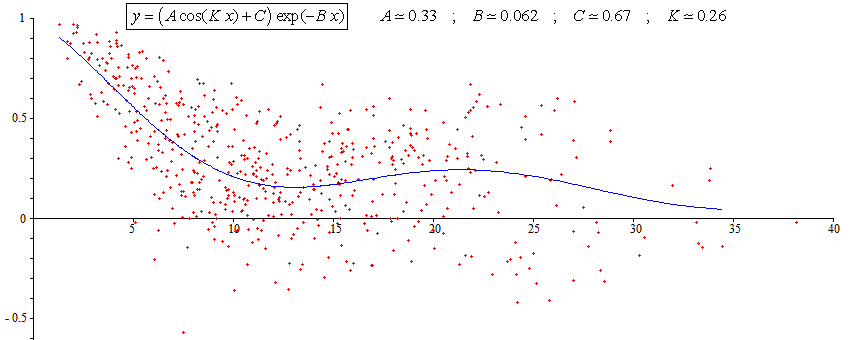
A significatively better fitting is obtained in adding the parameter C in the equation.
IN ADDITION in order to answer to somme comments :
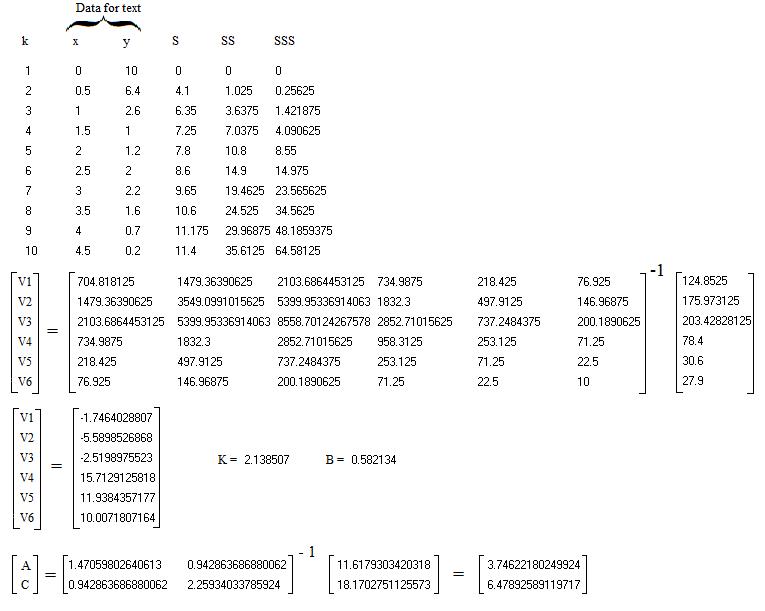
The method leading to the above result consists in two steps.
First step : a non-conventional method which is not iterative an doesn't requires initial "guessed" values of the parameters. The general principle is explained in this paper : 
It is not rare that people not familiar with this method make mistake in coding and say that the calculus fails. A lot of time is lost in discussions before the mistake be found and corrected. In order to avoid wasting time a "test" sheet is provided below. With the very small data it is easy for the user to check his code in comparing each intermediate numerical value to the correct values.
Then the method can be used with the big data given by the OP. The result is :
Don't be surprised that the values of the parameters are not exactly the same as the values given on the first figure at begining of my answer. This is because the criteria of fitting is not the same.
In his question the OP doesn't specify a criteria of fitting (LMSE, or LMAE, or LMSRE, or etc.). To each criteria of fitting correspond a different result. When the scatter is large the results can be very different one to the others. Since the scatter is very large in the present case, one cannot avoid to chose a particular criteria of fitting. If not the result is not unique. That is why a second step is necessary in the present case. But this not a general necessity.
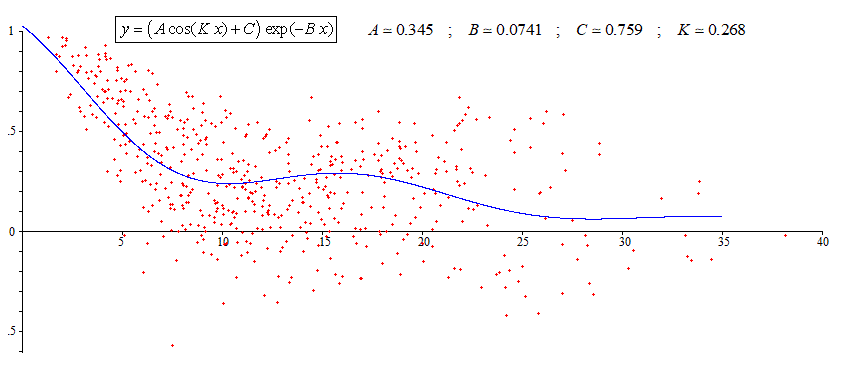
Second step (Eventually):
We have to chose a criteria of fitting. For example Least Mean Square Errors.
A non-linear method of regression (in which the chosen criteria is implemented) must be used. They are a lot of softwares. The calculus is iterative and one have to give some "guessed" initial values to start the itteration.
In case of large scatter the comvergence is not always good. The result might be far to be good with eventually failure if the initial values are not close to the correct values which are unknown. This is (partially) avoid thanks to the above first step. One can use the above values of K,B,A,C as rather good initial values. That is what was done to compute the values written on the first figure in my answer. This explains why the first figure is different from the last one.
NOTE :
To be honest one must acknowledge that the above method isn't infallible, especially in case of large scatter. I am surprized that a not too bad result be obtained. With three numerical integrations I was expecting much more difficulty. Certainly the large number of points is favourable. May be we are lucky with this data. We could have worse results with other set of data.