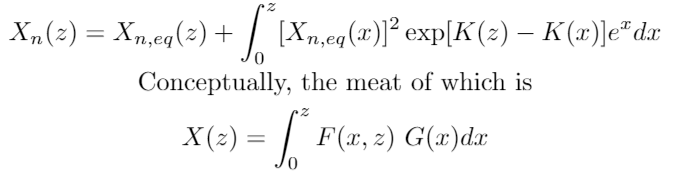Integrating a function of two variables over an array of values-CodePudding

I'm currently trying to solve this integral using SciPy:

I was first advised to use interpolation, which I tried but cannot figure out for some reason, but would probably be a good approach. I found this post about using np.vectorize and I think it might still work, but I am getting an error. Here is the code that I have written thus far (also note that n and n,eq are not indices, they're just variable names):

import numpy as np
from scipy import integrate 

def K(x): #This is a function in the integral.
    b = 0.252
    return b*(((4/(x**3)) (3/(x**2)) 1/x)   (4/(x**3)   1/(x**2))*np.exp(-x))

def Xntot_integrand(x,z): #Defining the integrand
    Xneq_x = (1 np.exp(x))**(-1) #This is the term outside the integral and squared within it.
    return Xneq_x(x)**2 * np.exp(K(z) - K(x)) * np.exp(x)

Xntot_integrand = np.vectorize(Xntot_integrand)

def Xntot_integrated(x,z):
    return quad(Xntot_integrand, 0, z)

Xntot_integrated=np.vectorize(Xntot_integrated)

T_narrow = np.linspace(1,0.01,100) #Narrow T range from 1 to 0.01 MeV
z_narrow = Q/T_narrow

final_integrated_Xneq = Xntot_integrated(z_narrow)

I am getting the error that I am missing a positional argument when I call Xntot_integrated (which makes sense, I think it is still in the two variables x and z).

So I suppose the issue is stemming from where I use quad() because after it is integrated, x should go away. Any advice? Should I use tabulation/interpolation instead?

CodePudding user response：

You need to be using the args keyword argument of integrate.quad to pass additional inputs to the function, so it would look like this:

def Xntot_integrated(z):
    return integrate.quad(Xntot_integrand, 0, z, args=(z,))

Note here x is not an input to the integrated function, only z, the first input to the integrand is the integration variable and any extra information is passed via args=(z,) tuple.

alternatively you can define a wrapper that knows z from context and only takes the integration variable as input:

def Xntot_integrated(z):
    def integrand(x):return Xntot_integrand(x,z)
    return integrate.quad(integrand, 0, z)

but most API's that take a function typically have a keyword argument to specify those inputs. (threading.Thread comes to mind.)

also your Xneq_x should probably be a function itself since you accidentally use it as such inside your integrand (it is just a value there right now) and you will need to use it outside the integration anyway :)