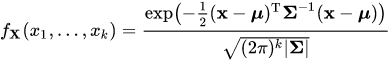R: Errors in Matrix Multiplication (non-conformable arguments)-CodePudding

I am working with the R programming language.

I have the following data:

1) Mean Vector (4 rows , 1 column)

4 variables (x1, x2, x3, x4)

2) Covariance Matrix (4 rows, 4 columns)

4 variables (diagonal elements are x1, x2, x3, x4 and pairwise elements are e.g 2nd element: (x1,x2), 3rd element (x1,x3), 4th element (x1, x4) etc.)

   0.15065114  0.13080115   0.02084463  0.01309107
   0.13080115  0.17604529   0.01603245  0.01221458
  0.02084463  0.01603245   0.02808260  0.00601568
  0.01309107  0.01221458   0.00601568  0.01042365

Question: I want to take the above data and create a function (with 4 inputs: x1, x2, x3, x4 and a single number as the output) in the following format:

Here is what I tried so far:

my_function <- function(x_one, x_two, x_three, x_four)

{


sigma1.pre <- c(0.15065114 , 0.13080115 ,  0.02084463 , 0.01309107 , 0.13080115 , 0.17604529 ,  0.01603245 , 0.01221458 , 0.02084463 , 0.01603245  , 0.02808260 , 0.00601568 , 0.01309107 , 0.01221458 ,  0.00601568 , 0.01042365)
sigma1 <- matrix(sigma1.pre, nrow=4, ncol= 4, byrow = TRUE)
sigma1_inv <- ginv(sigma1)
det_sigma1_inv <- det(sigma1_inv)
denom = sqrt( (2*pi)^4 * det_sigma1_inv) 

x_one = x1 - 5
x_two = x2 - 3.42
x_three = x3 - 1.462
x_four = x4 - 0.245

x_t = c(x_one, x_two, x_three, x_four)
x_t_one <- matrix(x_t, nrow=4, ncol= 1, byrow = TRUE)
x_t_one_t = -0.5 * t(x_t_one)
x_t_two =  matrix(x_t, nrow=1, ncol= 4, byrow = TRUE)

num = exp(x_t_two  %*%  sigma1_inv  %*%  x_t_one_t)

answer = num/denom

return(answer)
}

Problem: When I try to run this function:

my_function(1,2,3,4)

I get the following error:

Error in x_t_two %*% sigma1_inv %*% x_t_one_t : non-conformable arguments

I think that the error is occurring because of the matrix multiplication

num = exp(x_t_two  %*%  sigma1_inv  %*%  x_t_one_t)

I tried to change the order of the matrix multiplication:

num = exp( x_t_one_t   %*%  sigma1_inv  %*% x_t_two )

But the error is still there.

Can someone please show me how to fix this problem?

Thanks!

References:

CodePudding user response：

As I mentioned above, dmvnorm function returns the value of the function you show.

dmvnorm(c(5,3,1,0),m,v)
[1] 0.01074766

This is my manual version,

func <- function(vec, m, v){
  if (length(vec) != length(m)) {
    stop("dimension error")
  } # and several more
  a <- t(vec - m) %*% solve(v) %*% (vec - m)
  k <- length(vec)
  return(exp(-a/2)/sqrt((2*pi)^k * det(v)))
}

func(c(5,3,1,0) , m, v)
           [,1]
[1,] 0.01074766

In your function, the main reason that your function didn't work is in line num = exp(x_t_two %*% sigma1_inv %*% x_t_one_t), dimension of x_t_one_t was wrong. As you set this as nrow = 4, ncol = 1, it was already 4*1, you did not need to transpose that. I add some more comment on your function.

 my_function <- function(x_one, x_two, x_three, x_four)
  
{
  
  
  sigma1.pre <- c(0.15065114 , 0.13080115 ,  0.02084463 , 0.01309107 , 0.13080115 , 0.17604529 ,  0.01603245 , 0.01221458 , 0.02084463 , 0.01603245  , 0.02808260 , 0.00601568 , 0.01309107 , 0.01221458 ,  0.00601568 , 0.01042365)
  sigma1 <- matrix(sigma1.pre, nrow=4, ncol= 4, byrow = TRUE)
  # You can also use solve instead of ginv, solve is in base R
  sigma1_inv <- ginv(sigma1)
  det_sigma1_inv <- det(sigma1_inv)
  # In here, not det_sigma1_inv, just use det(sigma1) will work.
  denom = sqrt( (2*pi)^4 * det(sigma1)) 
  
  #in below part, I recommend another way.
  #m <- c( 5.0060022, 3.4280049, 1.4620007, 0.2459998)
  #x_t = c(x_one, x_two, x_three, x_four)
  #There was no input x1, x2, x3, x4
  x_one = x_one - 5.0060022
  x_two = x_two - 3.4280049
  x_three = x_three - 1.4620007
  x_four = x_four - 0.2459998
  
  
  # Vectors and matrices are handle as vector and matrices. You do not need to 
  #change vectors to matrices.
  #x_t_t = x_t - m
  x_t = c(x_one, x_two, x_three, x_four)
  x_t_one <- matrix(x_t, nrow=4, ncol= 1, byrow = TRUE)
  x_t_two =  matrix(x_t, nrow=1, ncol= 4, byrow = TRUE)
  
  
  # In this part, as it's (x-mu)^T * SIGMA * (x-mu), dimension of x_t_one_t was wrong
  # You may try another way.
  #num = exp(-0.5 * t(x_t_t) %*% sigma1_inv %*% x_t_t)
  num = exp(-0.5 * x_t_two  %*%  sigma1_inv  %*%  x_t)
  
  
  answer = num/denom
  
  return(answer)
}
my_function(5,3,1,0)
           [,1]
[1,] 0.01074766