Calculating mean and variance from a density kernel using Monte Carlo methods-CodePudding

Assuming a probability distribution has a density kernel of , what Monte Carlo methods can I use to estimate the mean and variance of the distribution?

CodePudding user response：

We can use numerical methods here. First of all, we create a function to represent your probability density function (though this is not yet scaled so that its integral is 1 over its full domain):

pdf <- function(x) x^2 * exp(-x^2/4)

plot(pdf, xlim = c(0, 10))

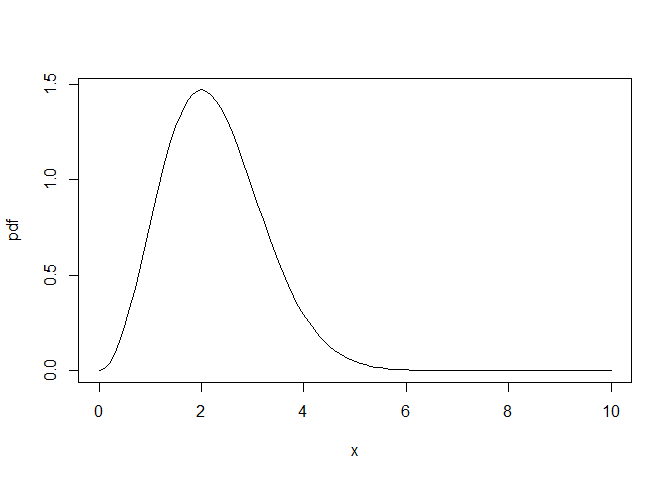
To get the scaling factor to turn this into a genuine pdf, we can integrate this function over its domain of c(0, Inf).

integrate(pdf, 0, Inf)$value
#> [1] 3.544908

So now we can generate a genuine pdf by dividing our original pdf by this amount:

pdf <- function(x)  x^2 * exp(-x^2/4) / 3.544908

plot(pdf, xlim = c(0, 10))

Now that we have a pdf, we can create a cdf with numerical integration:

cdf <- function(x) sapply(x, \(i) integrate(pdf, 0, i)$value)

plot(cdf, xlim = c(0, 10))

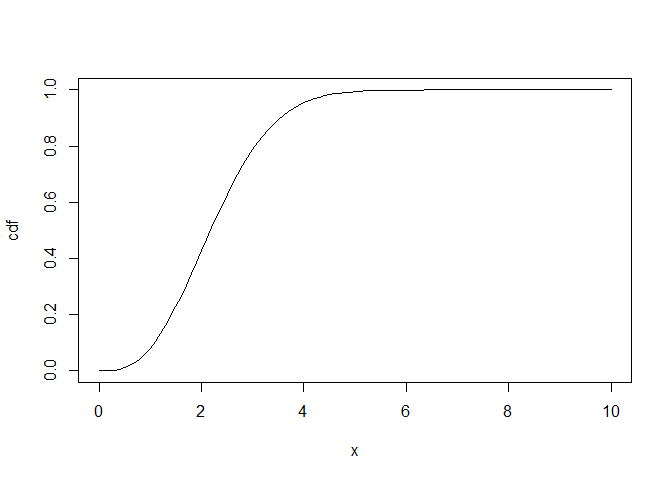
The inverse of the cdf is what we need, to be able to convert a sample taken from a uniform distribution between 0 and 1 into a sample drawn from our new distribution. We can create this inverse function using uniroot to find where the output of our cdf matches an arbitrary number between 0 and 1:

inverse_cdf <- function(p) 
{
  sapply(p, function(i) {
              uniroot(function(a) {cdf(a) - i}, c(0, 100))$root
  })
}

The inverse cdf looks like this:

plot(inverse_cdf, xlim = c(0, 0.99))

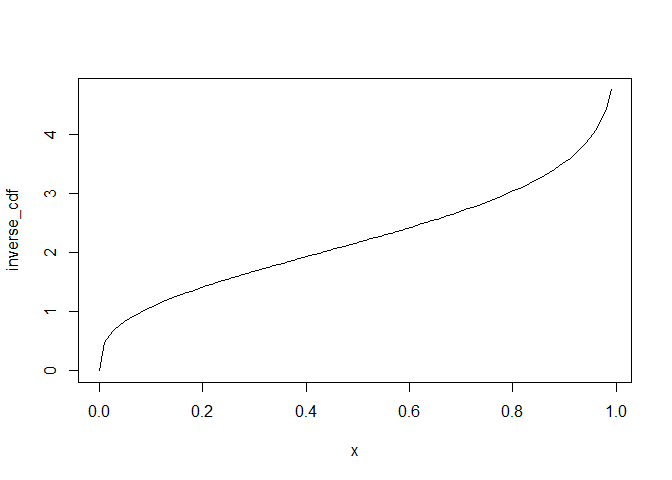
We are now ready to draw a sample from our distribution:

set.seed(1) # Makes this draw reproducible

x_sample <- inverse_cdf(runif(1000))

Now we can plot a histogram of our sample and ensure it matches the pdf:

hist(x_sample, freq = FALSE)

plot(function(x) pdf(x), add = TRUE, xlim = c(0, 6))

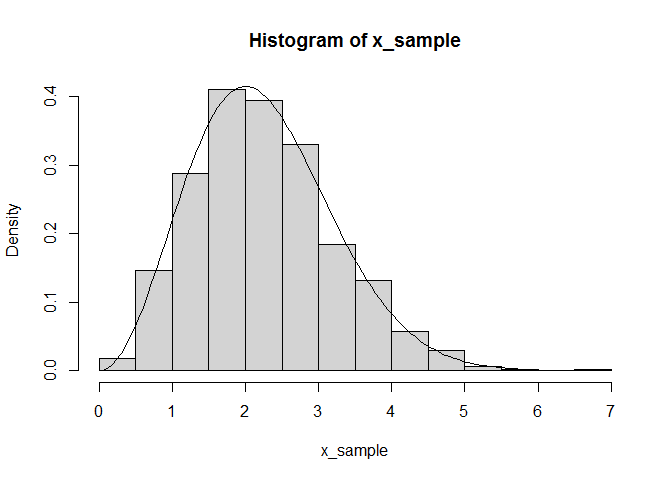
Now that we have a sample drawn from x, we can use the sample mean and variance as estimates for the distribution's mean and variance:

mean(x_sample)
#> [1] 2.264438

var(x_sample)
#> [1] 0.9265678

We can increase the accuracy of these estimates by taking larger and larger samples in our call to inverse_cdf(runif(1000)), by increasing the 1000 to a larger number.

^{Created on 2021-11-06 by the reprex package (v2.0.0)}