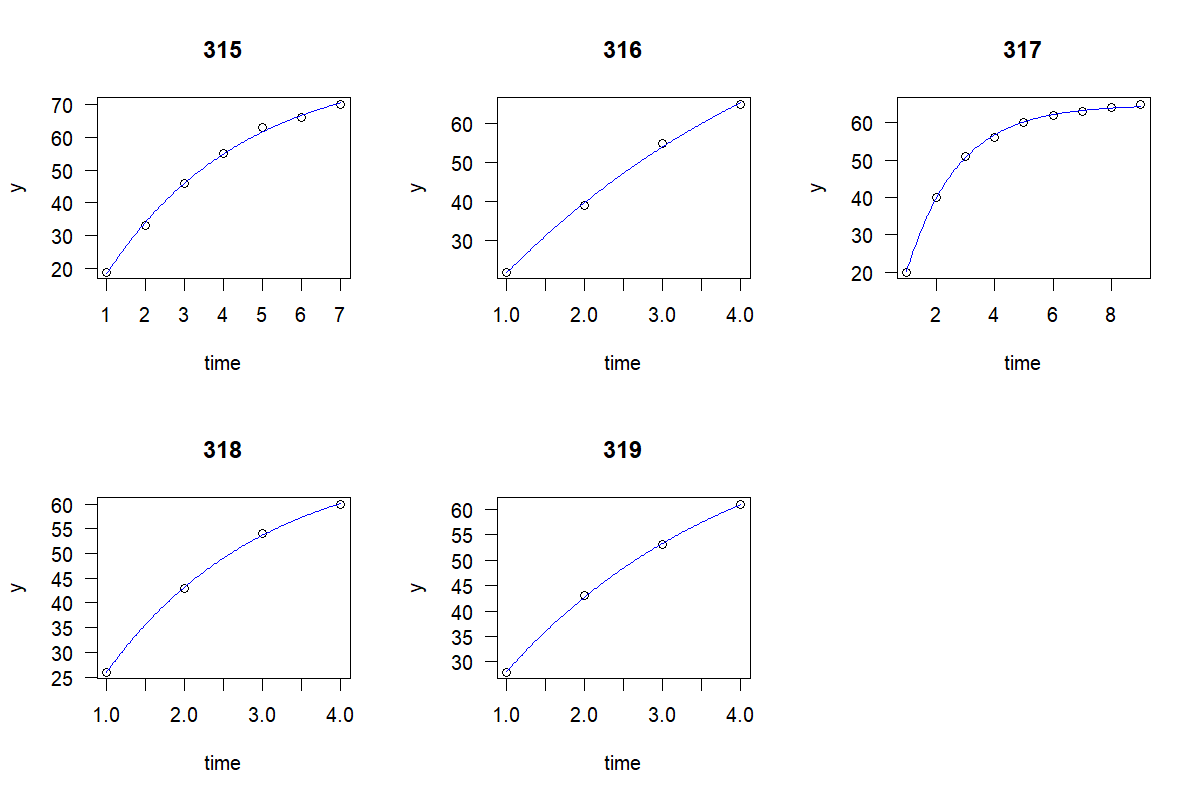I'm trying to fit a von Bertalanffy growth function (VGBF) in r to my data grouped by a serial number. This is a snippet of my data:

Serial_No<- c(315,315,315,315,315,315,315,316,316,316,316,317,317,317,317,317,317,317,317,317,318,318,318,318,319,319,319,319)

Year<-c(1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945)

tl<-c(19,33,46,55,63,66,70,22,39,55,65,20,40,51,56,60,62,63,64,65,26,43,54,60,28,43,53,61)

age<-c(1,2,3,4,5,6,7,1,2,3,4,1,2,3,4,5,6,7,8,9,1,2,3,4,1,2,3,4))

df<-data.frame(Serial_No, Year, tl, age)

I've been following this example: https://www.r-bloggers.com/2020/01/von-bertalanffy-growth-plots-ii/ and have changed my code to as follows:

vb <- vbFuns()
predict2 <- function(x) predict(x,data.frame(age=ages))

agesum <- group_by(df,Serial_No) %>%
summarize(minage=min(age),maxage=max(age))

Serial_Nos <- unique(df$Serial_No)
nSerial_Nos <- length(Serial_Nos)

cfs <- cis <- preds1 <- preds2 <- NULL

for (i in 1:nSerial_Nos) {
 cat(Serial_Nos[i],"Loop\n")
 tmp1 <- filter(df,Serial_No==Serial_Nos[i])
 sv1 <- vbStarts(tl~age,data=tmp1)
 fit1 <- nls(tl~vb(age,Linf,K,t0),data=tmp1,start=sv1)
 cfs <- rbind(cfs,coef(fit1))
 boot1 <- Boot(fit1)
 tmp2 <-  confint(boot1)
 cis <- rbind(cis,c(tmp2["Linf",],tmp2["K",],tmp2["t0",]))
 ages <- seq(-1,16,0.2)
 boot2 <- Boot(fit1,f=predict2)
 tmp2 <- data.frame(Serial_No=Serial_Nos[i],age=ages,
                 predict(fit1,data.frame(age=ages)),
                 confint(boot2))
 preds1 <- rbind(preds1,tmp2)
 tmp2 <- filter(tmp2,age>=agesum$minage[i],age<=agesum$maxage[i])
 preds2 <- rbind(preds2,tmp2)
}

The code runs, but the results from the VBGF returned are the same for every serial no, which can't be the case. I think it's the filter function not working in the above code.

I've searched for solutions but can't get it to work.

If anyone can please help, or knows of a solution i'd really appreciate it.

Thank you in advance

CodePudding user response：

Model fit with package growthrates

The following post describes an alternative approach without for-loop and filter. Similar loop-free solutions can be implemented using the common nls function and lapply in "base" R or group_by in "tidyverse".

Model definition

The growthrates package does not contain a von Bertalanffy function, so it has to be provided as user supplied model, as described in the package vignette. Here I borrowed the function from package FSA and adapted it accordingly:

library("growthrates")

grow_von_bert <- function(time, parms) {
  with(as.list(parms), {
    y <- Linf * (1 - exp(-K * (time - t0)))
    as.matrix(data.frame(time = time, y = y))
  })
}

Test of the model with a single example

p <- c(t0=5, Linf=10, K=.1)
time <- seq(5, 100)
plot(grow_von_bert(time, p), type="l")

Fit of a single data example

It is always a good idea to fit one or more single examples first, before doing this for all.

df1 <- subset(df, Serial_No == 315)
fit1 <- fit_growthmodel(df1$age, df1$tl,
                        FUN = grow_von_bert,  p=c(t0=0, Linf=70, K=0.1))
summary(fit1)

Fit of all data sets

This can be done in a loop or with appropriate tidyverse functions, whipe package growthrates has such a function already built in, so all models can be fitted with a single function call. It is of course necessary to specify good start parameters, either the same for all curves or individual parameter sets, depending on the quality of the data. Here is the complete code including the data of the OP:

library("growthrates")

df <- data.frame(
  Serial_No = factor(c(315,315,315,315,315,315,315,316,316,316,316,317,317,317,317,
                       317,317,317,317,317,318,318,318,318,319,319,319,319)),
  year = c(1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,
          1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945,1945),
  tl = c(19,33,46,55,63,66,70,22,39,55,65,20,40,51,56,60,62,63,64,65,26,43,54,60,28,
         43,53,61),
  age = c(1,2,3,4,5,6,7,1,2,3,4,1,2,3,4,5,6,7,8,9,1,2,3,4,1,2,3,4)
)

grow_von_bert <- function(time, parms) {
  with(as.list(parms), {
    y <- Linf * (1 - exp(-K * (time - t0)))
    as.matrix(data.frame(time = time, y = y))
  })
}


fit <- all_growthmodels(tl ~ age | Serial_No, 
                        data=df, 
                        FUN = grow_von_bert,
                        p=c(t0=0, Linf=70, K=0.1))

results(fit)
par(mfrow=c(2,3))
plot(fit, las=1)