Phase portrait of Verhulst equation-CodePudding

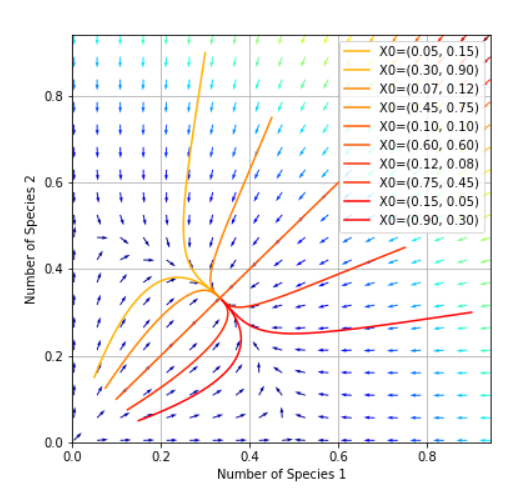
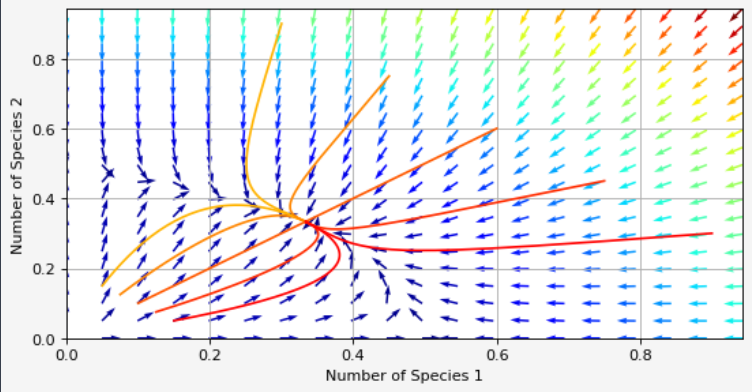
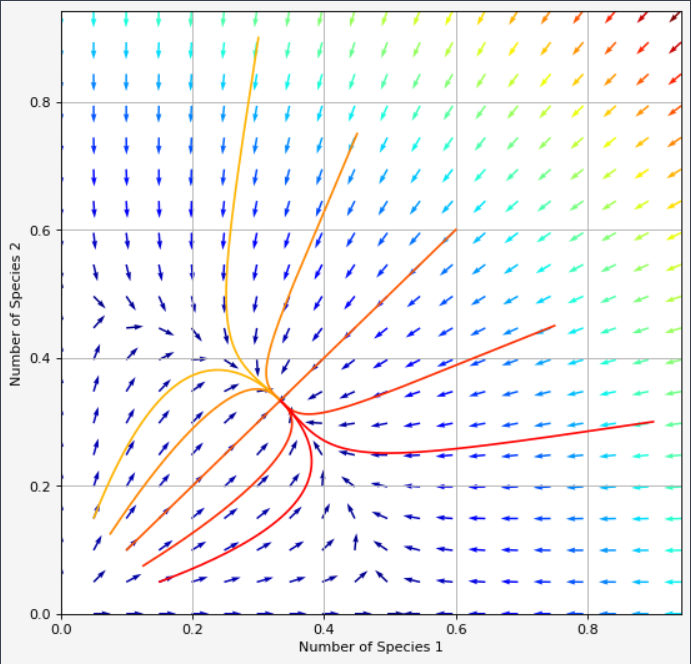
I was trying to an example of the book -"Dynamical Systems with Applications using Python" and I was asked to plot the phase portrait of Verhulst equation, then I came across this post:

That is still different from:

What am I missing?

CodePudding user response：

With the help of @Lutz Lehmann I could rewrite the code to get want I needed.

The solutions is something like this:

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

fig = plt.figure(figsize=(8, 4), dpi= 80, facecolor='whitesmoke', edgecolor='k')
beta, delta, gamma = 1, 2, 1
b,d,c = 1,2,1

t = np.linspace(0, 10, 100)

C1 = gamma*c-delta*d
C2 = gamma*b-beta*d
C3 = beta*c-delta*b

def verhulst(X, t=0):
    return np.array([beta*X[0] - delta*X[0]**2 -gamma*X[0]*X[1],
                     b*X[1] - d*X[1]**2 -c*X[0]*X[1]])

X_O = np.array([0., 0.])
X_R = np.array([C2/C1, C3/C1])
X_P = np.array([0, b/d])
X_Q = np.array([beta/delta, 0])

def jacobian(X, t=0):
    return np.array([[beta-delta*2*X[0]-gamma*X[1],  -gamma*x[0]],
                     [b-d*2*X[1]-c*X[0],             -c*X[1]]])

values  = np.linspace(0.05, 0.15, 5)                      
vcolors = plt.cm.autumn_r(np.linspace(0.3, 1., len(values)))


for v, col in zip(values, vcolors):
    X0 = [v,0.2-v]
    X = odeint(verhulst, X0, t)
    plt.plot(X[:,0], X[:,1], color=col, label='X0=(%.f, %.f)' % ( X0[0], X0[1]) )

for v, col in zip(values, vcolors):
    X0 = [6 * v, 6 *(0.2-v)]
    X = odeint(verhulst, X0, t)
    plt.plot(X[:,0], X[:,1], color=col, label='X0=(%.f, %.f)' % ( X0[0], X0[1]) )

    
ymax = plt.ylim(ymin=0)[1] 
xmax = plt.xlim(xmin=0)[1]
nb_points = 20

x = np.linspace(0, xmax, nb_points)
y = np.linspace(0, ymax, nb_points)

X1, Y1  = np.meshgrid(x, y)
DX1, DY1 = verhulst([X1, Y1])  # compute growth rate on the gridt
M = (np.hypot(DX1, DY1))       # Norm of the growth rate
M[M == 0] = 1.                 # Avoid zero division errors
DX1 /= M                       # Normalize each arrows
DY1 /= M

plt.quiver(X1, Y1, DX1, DY1, M, cmap=plt.cm.jet)
plt.xlabel('Number of Species 1')
plt.ylabel('Number of Species 2')
plt.grid()

We get what we were looking for:

Finally, I would like to thank again @Lutz Lehnmann for the help. I wouldn't have solved without it him.

Edit 1:

I forgot $t = np.linspace(0, 10, 100)$ and if you change figsize = (8,8), we get a nicer shape in the plot. (Thank you @Trenton McKinney for the remarks)