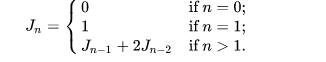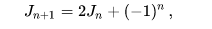Jacobsthal number recursion formula-CodePudding

I have a very simple (and stupid :) question:

How do I get from this expression:

To this recursion formula?

I do not want any complete solution, but maybe you can help me to understand it with just a few tips.

Thx, and a nice day :)

CodePudding user response：

This is very similar to [Wikipedia]: Fibonacci number, and is a typical [Wikipedia]: Mathematical induction example.

Starting from the assumption that the formula is true for (a given) n (let's call this P(n)):

J_n = 2 * J_{n - 1} (-1)^{n - 1}

then, using the above equality and the function definition, you must prove P(n 1) - that the formula is also true for (the consecutive) n 1. This is the one in your question:

J_{n 1} = 2 * J_n (-1)ⁿ

Since this is a programming site (and I'm too lazy calculating the first few values manually), here's some Python code that does that for us:

>>> def j(n):
...     if n <= 0:
...         return 0
...     elif n == 1:
...         return 1
...     else:
...         return j(n - 1)   2 * j(n - 2)
... 
>>>
>>> for i in range(15):
...     print("{:2d} - {:4d}".format(i, j(i)))
...
 0 -    0
 1 -    1
 2 -    1
 3 -    3
 4 -    5
 5 -   11
 6 -   21
 7 -   43
 8 -   85
 9 -  171
10 -  341
11 -  683
12 - 1365
13 - 2731
14 - 5461

From the above, it's kind of noticeable by the naked eye that the formula is true.
Now the induction mechanism should be applied: start from P(n) and using the function definition (3^rd branch) get to P(n 1). That might not be trivial, considering there's a level 2 dependency (most of the terms that will eventually reduce each other, but I didn't try it to see how "visible" that would be).
You could check [SO]: Recursive summation of a sequence returning wrong result (@CristiFati's answer), for more details on a simpler problem.

Note:

Given the current coefficients, I must mention recursion's characteristic equation (check [\Wikipedia]: Constant-recursive sequence) that would give a non recurring formula for J_n:

J_n = J_{n - 1} 2 * J_{n - 2} translates to: x² = x¹ 2 * x⁰ -> x² - x - 2 = 0 (which has -1 and 2 as roots), and from here (using Binet (or Moivre) formula):

J_n = (2ⁿ - (-1)ⁿ) / 3 (denominator value is: 2 - -1)

Let the computer do some calculations from us (check that previous implementation results match this one's):

>>> def j_simpl(n):
...     return (2 ** n - (-1) ** n) / 3
...
>>>
>>> print(all(j(i) == j_simpl(i) for i in range(20)))
True