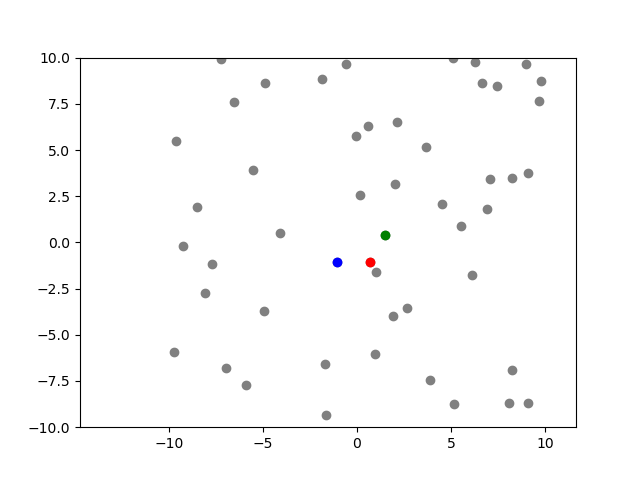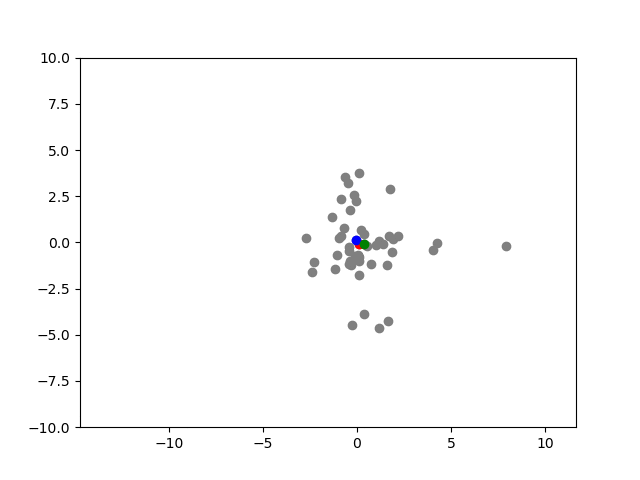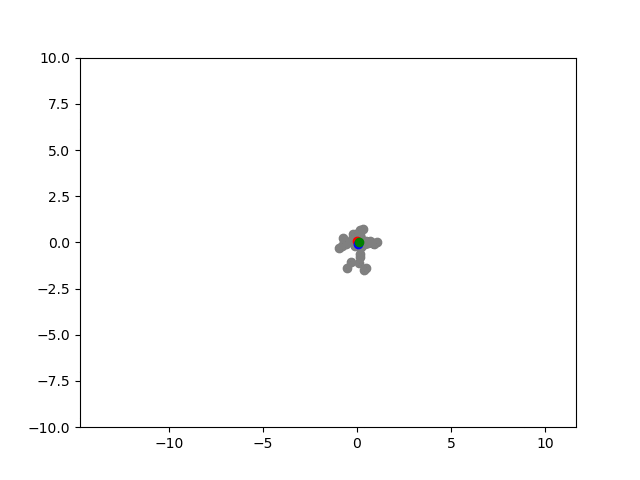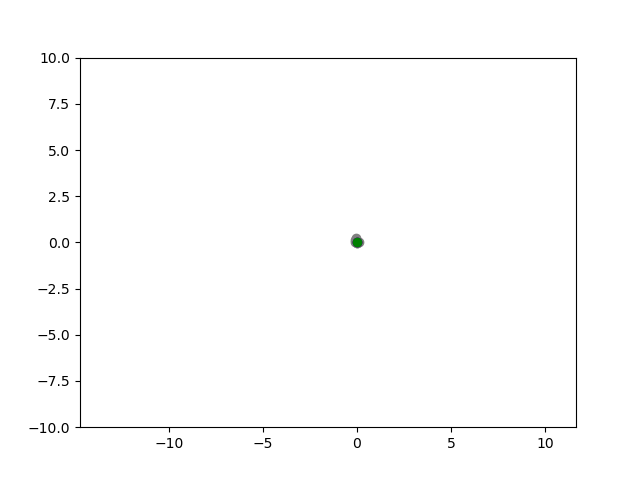
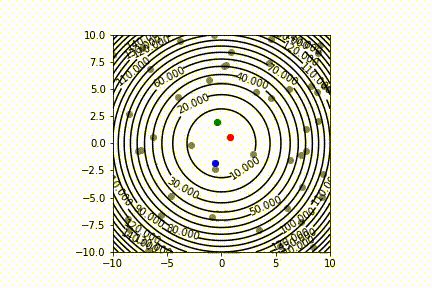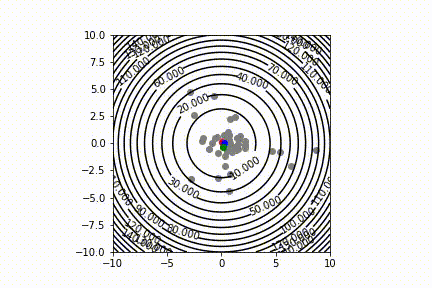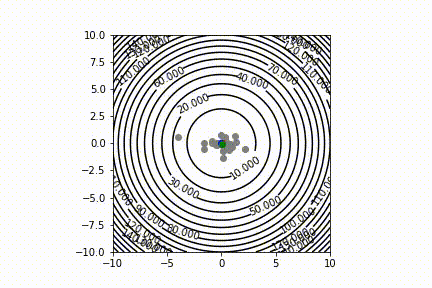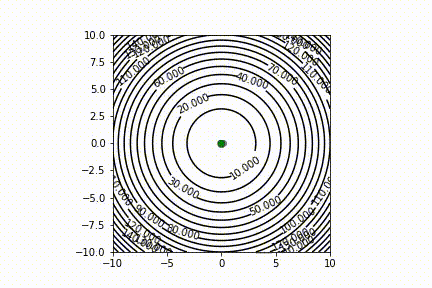
I have implemented a simple randomized, population-based optimization method - Grey Wolf optimizer. I am having some trouble with properly capturing the Matplotlib plots at each iteration using the camera package.
I am running GWO for the objective function f(x,y) = x^2 y^2. I can only see the candidate solutions converging to the minima, but the contour plot doesn't show up.
Do you have any suggestions, how can I display the contour plot in the background?
GWO Algorithm implementation
%matplotlib notebook
import matplotlib.pyplot as plt
import numpy as np
from celluloid import Camera
import ffmpeg
import pillow
# X : Position vector of the initial population
# n : Initial population size
def gwo(f,max_iterations,LB,UB):
fig = plt.figure()
camera = Camera(fig)
def random_population_uniform(m,a,b):
dims = len(a)
x = [list(a np.multiply(np.random.rand(dims),b - a)) for i in range(m)]
return np.array(x)
def search_agent_fitness(fitness):
alpha = 0
if fitness[1] < fitness[alpha]:
alpha, beta = 1, alpha
else:
beta = 1
if fitness[2] > fitness[alpha] and fitness[2] < fitness[beta]:
beta, delta = 2, beta
elif fitness[2] < fitness[alpha]:
alpha,beta,delta = 2,alpha,beta
else:
delta = 2
for i in range(3,len(fitness)):
if fitness[i] <= fitness[alpha]:
alpha, beta,delta = i, alpha, beta
elif fitness[i] > fitness[alpha] and fitness[i]<= fitness[beta]:
beta,delta = i,beta
elif fitness[i] > fitness[beta] and fitness[i]<= fitness[delta]:
delta = i
return alpha, beta, delta
def plot_search_agent_positions(f,X,alpha,beta,delta,a,b):
# Plot the positions of search agents
x = X[:,0]
y = X[:,1]
s = plt.scatter(x,y,c='gray',zorder=1)
s = plt.scatter(x[alpha],y[alpha],c='red',zorder=1)
s = plt.scatter(x[beta],y[beta],c='blue',zorder=1)
s = plt.scatter(x[delta],y[delta],c='green',zorder=1)
camera.snap()
# Initialize the position of the search agents
X = random_population_uniform(50,np.array(LB),np.array(UB))
n = len(X)
l = 1
# Plot the first image on screen
x = np.linspace(LB[0],LB[1],1000)
y = np.linspace(LB[0],UB[1],1000)
X1,X2 = np.meshgrid(x,y)
Z = f(X1,X2)
cont = plt.contour(X1,X2,Z,20,linewidths=0.75)
while (l < max_iterations):
# Take the x,y coordinates of the initial population
x = X[:,0]
y = X[:,1]
# Calculate the objective function for each search agent
fitness = list(map(f,x,y))
# Update alpha, beta and delta
alpha,beta,delta = search_agent_fitness(fitness)
# Plot search agent positions
plot_search_agent_positions(f,X,alpha,beta,delta,LB,UB)
# a decreases linearly from 2 to 0
a = 2 - l *(2 / max_iterations)
# Update the position of search agents including the Omegas
for i in range(n):
x_prey = X[alpha]
r1 = np.random.rand(2) #r1 is a random vector in [0,1] x [0,1]
r2 = np.random.rand(2) #r2 is a random vector in [0,1] x [0,1]
A1 = 2*a*r1 - a
C1 = 2*r2
D_alpha = np.abs(C1 * x_prey - X[i])
X_1 = x_prey - A1*D_alpha
x_prey = X[beta]
r1 = np.random.rand(2)
r2 = np.random.rand(2)
A2 = 2*a*r1 - a
C2 = 2*r2
D_beta = np.abs(C2 * x_prey - X[i])
X_2 = x_prey - A2*D_beta
x_prey = X[delta]
r1 = np.random.rand(2)
r2 = np.random.rand(2)
A3 = 2*a*r1 - a
C3 = 2*r2
D_delta = np.abs(C3 * x_prey - X[i])
X_3 = x_prey - A3*D_delta
X[i] = (X_1 X_2 X_3)/3
l = l 1
return X[alpha],camera
Function call
# define the objective function
def f(x,y):
return x**2 y**2
minimizer,camera = gwo(f,7,[-10,-10],[10,10])
animation = camera.animate(interval = 1000, repeat = True,
repeat_delay = 500)
CodePudding user response:
Is it possible that the line x = np.linspace(LB[0],LB[1],1000) should be x = np.linspace(LB[0],UB[1],1000) instead? With your current definition of x, x is an array only filled with the value -10 which means that you are unlikely to find a contour.
Another thing that you might want to do is to move the cont = plt.contour(X1,X2,Z,20,linewidths=0.75) line inside of your plot_search_agent_positions function to ensure that the contour is plotted at each iteration of the animation.
Once you make those changes, the code looks like that:
import matplotlib.pyplot as plt
import numpy as np
from celluloid import Camera
import ffmpeg
import PIL
from matplotlib import animation, rc
from IPython.display import HTML, Image # For GIF
from scipy.interpolate import griddata
rc('animation', html='html5')
# X : Position vector of the initial population
# n : Initial population size
def gwo(f,max_iterations,LB,UB):
fig = plt.figure()
fig.gca(aspect='equal')
camera = Camera(fig)
def random_population_uniform(m,a,b):
dims = len(a)
x = [list(a np.multiply(np.random.rand(dims),b - a)) for i in range(m)]
return np.array(x)
def search_agent_fitness(fitness):
alpha = 0
if fitness[1] < fitness[alpha]:
alpha, beta = 1, alpha
else:
beta = 1
if fitness[2] > fitness[alpha] and fitness[2] < fitness[beta]:
beta, delta = 2, beta
elif fitness[2] < fitness[alpha]:
alpha,beta,delta = 2,alpha,beta
else:
delta = 2
for i in range(3,len(fitness)):
if fitness[i] <= fitness[alpha]:
alpha, beta,delta = i, alpha, beta
elif fitness[i] > fitness[alpha] and fitness[i]<= fitness[beta]:
beta,delta = i,beta
elif fitness[i] > fitness[beta] and fitness[i]<= fitness[delta]:
delta = i
return alpha, beta, delta
def plot_search_agent_positions(f,X,alpha,beta,delta,a,b,X1,X2,Z):
# Plot the positions of search agents
x = X[:,0]
y = X[:,1]
s = plt.scatter(x,y,c='gray',zorder=1)
s = plt.scatter(x[alpha],y[alpha],c='red',zorder=1)
s = plt.scatter(x[beta],y[beta],c='blue',zorder=1)
s = plt.scatter(x[delta],y[delta],c='green',zorder=1)
Z=f(X1,X2)
cont=plt.contour(X1,X2,Z,levels=20,colors='k',norm=True)
plt.clabel(cont, cont.levels, inline=True, fontsize=10)
camera.snap()
# Initialize the position of the search agents
X = random_population_uniform(50,np.array(LB),np.array(UB))
n = len(X)
l = 1
# Plot the first image on screen
x = np.linspace(LB[0],UB[1],1000)
y = np.linspace(LB[0],UB[1],1000)
X1,X2 = np.meshgrid(x,y)
Z=f(X1,X2)
while (l < max_iterations):
# Take the x,y coordinates of the initial population
x = X[:,0]
y = X[:,1]
# Calculate the objective function for each search agent
fitness = list(map(f,x,y))
# Update alpha, beta and delta
alpha,beta,delta = search_agent_fitness(fitness)
# Plot search agent positions
plot_search_agent_positions(f,X,alpha,beta,delta,LB,UB,X1,X2,Z)
# a decreases linearly from 2 to 0
a = 2 - l *(2 / max_iterations)
# Update the position of search agents including the Omegas
for i in range(n):
x_prey = X[alpha]
r1 = np.random.rand(2) #r1 is a random vector in [0,1] x [0,1]
r2 = np.random.rand(2) #r2 is a random vector in [0,1] x [0,1]
A1 = 2*a*r1 - a
C1 = 2*r2
D_alpha = np.abs(C1 * x_prey - X[i])
X_1 = x_prey - A1*D_alpha
x_prey = X[beta]
r1 = np.random.rand(2)
r2 = np.random.rand(2)
A2 = 2*a*r1 - a
C2 = 2*r2
D_beta = np.abs(C2 * x_prey - X[i])
X_2 = x_prey - A2*D_beta
x_prey = X[delta]
r1 = np.random.rand(2)
r2 = np.random.rand(2)
A3 = 2*a*r1 - a
C3 = 2*r2
D_delta = np.abs(C3 * x_prey - X[i])
X_3 = x_prey - A3*D_delta
X[i] = (X_1 X_2 X_3)/3
l = l 1
return X[alpha],camera
# define the objective function
def f(x,y):
return x**2 y**2
minimizer,camera = gwo(f,7,[-10,-10],[10,10])
animation = camera.animate(interval = 1000, repeat = True,repeat_delay = 500)
And the output gives: