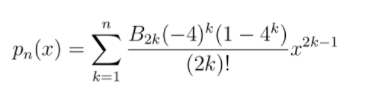I'm trying to calculate the nth term but its giving me wrong answers

import math

def bernoulli(m):
    if m == 0:
        return 1
    else:
        t = 0
        for k in range(0, m):
            t  = math.comb(m, k) * bernoulli(k) / (m - k   1)
        return 1 - t

def pn(n, x):
    sum = 0
    for i in range(n):
        sum  = ((bernoulli(2 * i)) / math.factorial(2 * i)) * (-4**i) * (1 - (4**i)) * (x**((2 * i) - 1))

Equation:

CodePudding user response：

Here are a few comments:

• In python, the convention is to include the start, and exclude the end. list(range(1,4)) is only [1, 2, 3], not [1,2,3,4]. Thus your Bernouilli loop should be for k in range(0, m 1) and your pn loop should be for i in range(1, n 1).
• Exponentiation has a higher precedence than most operators. -4**i is parsed as -(4**i), not as (-4)**i.
• sum is already the name of a builtin function in python. It is very strongly advised not to shadow the names of builtins. Call that variable s or total or something else, not sum.

Finally, the code becomes:

import math

def bernoulli(m):
    if m == 0:
        return 1
    else:
        t = 0
        for k in range(0, m 1):
            t  = math.comb(m, k) * bernoulli(k) / (m - k   1)
        return 1 - t

def pn(n, x):
    s = 0
    for i in range(1, n 1):
        s  = ((bernoulli(2 * i)) / math.factorial(2 * i)) * ((-4)**i) * (1 - (4**i)) * (x**(2 * i - 1))
    return s

And, using builtin function sum:

import math

def bernoulli(m):
    if m == 0:
        return 1
    else:
        return 1 - sum(math.comb(m, k) * bernoulli(k) / (m - k   1)
                       for k in range(0, m 1))

def pn(n, x):
    return sum((bernoulli(2 * i)) / math.factorial(2 * i)) * ((-4)**i) * (1 - (4**i)) * (x**(2 * i - 1)
               for i in range(1, n 1))