Graph representations in Prolog-CodePudding

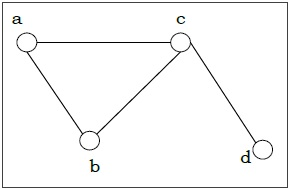
Consider the following graph

and that it is described by the below Prolog term :

graph([connected(a,[b,c]), connected(b,[a,c]), connected(c,[a,b,d]), connected(d,[c]) ]).

I would like to define a predicate which transforms the above connections into a list of the corresponding pairs. In other words, a predicate which yields [[a,b],[a,c],[b,c],[c,d]] for the above term-graph.

Could you please advise how to do it ?

My attempt so far is the following :

map 2-neighbor vertex to pairs :

map2ne(adjacent(H,[K|T]),Pair) :-
    append([H],[K],L),
    append([H],T,M),
    append([L],[M],Pair).

This runs ok.

map 3-neighbor vertex to pairs :

map3n(adjacent(H,[K,L|T]),Pair) :-
    append([H],[K],A1),
    append([H],[L],A2),
    append([A1],[A2],Z),
    append([H],T,M),
    append(Z,[M],Pair).

This also runs ok.

But when I try to extend it to n-neighbor vertex, then it fails :

mapmany(adjacent(H, [K|_]),Pair) :-
    append([H],[K],L),
    append(L,[],Pair),
    mapmany(adjacent(H,[K|_]),M),
    append(M,Pair,Pair).

And also the below fails, which was intented to map many n-neighbor vertices to pairs :

mapping(Map,Pairs) :-
    select(X,Map,Y),
    mapmany(X,PairX),
    append([PairX],Pairs),
    mapping(Y,Pairs).

CodePudding user response：

There are too many flaws in your code:

The adjacency list defined by graph/1 is composed of terms of the form connected(Vertex, Neighbors); however, your code deals with an adjacency list of terms of the form adjacent(Vertex, Neighbors).
Predicate append/3 should not be used to create all lists; for example, instead of append([H], [K], L), you should use L = [H, K].
In Prolog, it is more idiomatic to represent a pair of items V and W as V-W, instead of [V,W].
By the answer you expect for the example given (i.e., [a-b,a-c,b-c,c-d]), a single term V-W (i.e., {V,W}) represents both the edges (V,W) and (W,V). So, to avoid redundancy, you must exclusively choose V-W or W-V to put in your answer (without loss of generality, you can choose the term where V precedes W).

To to create an edge, you can do the following:

edge(V, W, Edge) :-
    (   V @< W
    ->  Edge = V-W
    ;   Edge = W-V ).

Examples:

?- edge(a, b, Edge).
Edge = a-b.

?- edge(b, a, Edge).
Edge = a-b.

To create all edges connecting a vertex V to its neighbors Ns, without duplicates, just ask:

?- V=a, Ns=[b,c,d], setof(E, W^Ns^(member(W,Ns), edge(V,W,E)), Edges).
V = a,
Ns = [b, c, d],
Edges = [a-b, a-c, a-d].

Notice that the construct Var^Goal tells setof/3 not to bind variable Var in Goal (in other words, indicates that Var is existentially quantified).

Generalizing this idea, we have:

graph_edges(Graph, Edges) :-
    setof( Edge,
           V^Ns^W^( member(connected(V, Ns), Graph),
                    member(W, Ns),
                    edge(V, W, Edge)),
           Edges ).

graph([connected(a, [b, c]),
       connected(b, [a, c]),
       connected(c, [a, b, d]),
       connected(d, [c])]).

Example:

?- graph(G), graph_edges(G, E).
G = [connected(a, [b, c]), connected(b, [a, c]), connected(c, [a, b, d]), connected(d, [c])],
E = [a-b, a-c, b-c, c-d].

LIBRARY UGRAPHS

In SWI-Prolog, a trivial solution would be to use the predicate edges/2 from library(ugraphs). Be careful though, because the representation of undirected graphs on which the predicate edge/2 is based is different from the one you are considering (an undirected graph in the library(ugraphs) is represented by a list of vertex pairs where the order of the vertices in these pairs matters). For example:

?- edges([a-[b,c], b-[a,c], c-[a,b,d], d-[c]], E).
E = [a-b, a-c, b-a, b-c, c-a, c-b, c-d, d-c].