How to get the coordinates of the following point knowing two previous points and the distance to th-CodePudding

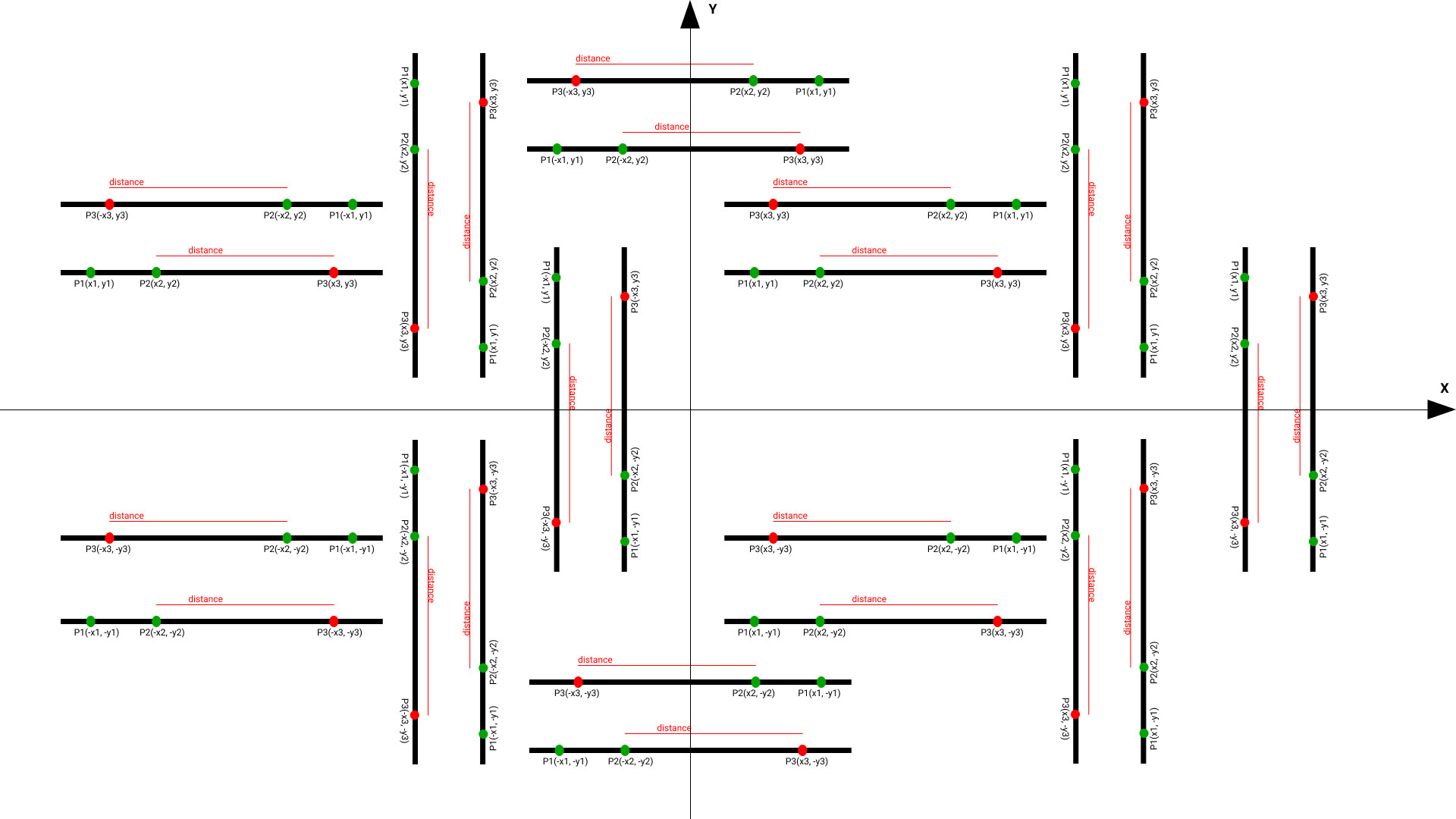
I am wondering how to find the coordinates of the following point If I know two previous points and distance to the following point. For example:

-----P1------P2----d---P3-----

Data:

P1: { x: 0, y: 1 }
P2: { x: 2, y: 1 }
d: 2

Searched:

P3: x3?, y3?

For this example, the result will be P3: { x: 4, y: 1 }. This is a straightforward calculation. Things get complicated when P1 and P2 are in different quadrant's, the direction of following point is changing or the line is under some tilts angle(for this I do not have any tests yet).

All these possibilities can be described by below picture(excluding these with line under some tilted angle):

For now, I end up with such algorithm:

interface Coordinates {
    x: number,
    y: number,
}

function getCoordinatesOfFollowingPointInDistanceToLastPointOnLine (p1: Coordinates, p2: Coordinates,
    distance: number): Coordinates {
    const lineSlope = (p2.y - p1.y) / (p2.x - p1.x);
    const lineTiltAngle = Math.atan(lineSlope);
    const p3x = Math.abs(p1.x)   Math.abs(p2.x) > Math.abs(p1.x)
        ? p2.x   distance * Math.cos(lineTiltAngle)
        : p2.x - distance * Math.cos(lineTiltAngle);
    const p3y = Math.abs(p1.y)   Math.abs(p2.y) > Math.abs(p1.y)
        ? p2.y   distance * Math.sin(lineTiltAngle)
        : p2.y - distance * Math.sin(lineTiltAngle);

    return {
        x: Number(p3x.toFixed(3)),
        y: Number(p3y.toFixed(3))
    };
}

I have test my algorithm, and it doesn't work in some cases(when line is horizontal and following point is in -∞ direction). All tests are shown below:

  getCoordinatesOfFollowingPointInDistanceToLastPointOnLine
    Orientation Horizontal
      Following point in  ∞ direction
        √ should calculate correctly position of P3 if P1 and P2 are in I quadrant (2 ms)
        √ should calculate correctly position of P3 if P1 and P2 are in II quadrant (1 ms)
        √ should calculate correctly position of P3 if P1 and P2 are in III quadrant
        √ should calculate correctly position of P3 if P1 and P2 are in IV quadrant (1 ms)
        √ should calculate correctly position of P3 if P1 in quadrant II and P2 in quadrant I (1 ms)
        √ should calculate correctly position of P3 if P1 in quadrant IV and P2 in quadrant III (4 ms)
      Following point in -∞ direction
        × should calculate correctly position of P3 if P1 and P2 are in I quadrant (4 ms)
        × should calculate correctly position of P3 if P1 and P2 are in II quadrant (1 ms)
        × should calculate correctly position of P3 if P1 and P2 are in III quadrant (1 ms)
        × should calculate correctly position of P3 if P1 and P2 are in IV quadrant
        × should calculate correctly position of P3 if P1 in quadrant I and P2 in quadrant II
        × should calculate correctly position of P3 if P1 in quadrant III and P2 in quadrant IV (1 ms)
    Orientation Vertical
      Following point in  ∞ direction
        √ should calculate correctly position of P3 if P1 and P2 are in I quadrant
        √ should calculate correctly position of P3 if P1 and P2 are in II quadrant
        √ should calculate correctly position of P3 if P1 and P2 are in III quadrant (1 ms)
        √ should calculate correctly position of P3 if P1 and P2 are in IV quadrant
        √ should calculate correctly position of P3 if P1 in quadrant IV and P2 in quadrant I
        √ should calculate correctly position of P3 if P1 in quadrant III and P2 in quadrant II (1 ms)
      Following point in -∞ direction
        √ should calculate correctly position of P3 if P1 and P2 are in I quadrant (1 ms)
        √ should calculate correctly position of P3 if P1 and P2 are in II quadrant
        √ should calculate correctly position of P3 if P1 and P2 are in III quadrant
        √ should calculate correctly position of P3 if P1 and P2 are in IV quadrant
        √ should calculate correctly position of P3 if P1 in quadrant I and P2 in quadrant IV (1 ms)
        √ should calculate correctly position of P3 if P1 in quadrant II and P2 in quadrant III

Tests Code:

// Orientation Horizontal -> Following point in  ∞ direction
test('should calculate correctly position of P3 if P1 and P2 are in I quadrant', () => {
    const p1: Coordinates = { x: 0, y: 1 };
    const p2: Coordinates = { x: 2, y: 1 };
    const p3 = getCoordinatesOfFollowingPointInDistanceToLastPointOnLine(p1, p2, 2);

    expect(p3.x).toBe(4);
    expect(p3.y).toBe(1);
});
// Orientation Horizontal -> Following point in -∞ direction
test('should calculate correctly position of P3 if P1 and P2 are in I quadrant', () => {
    const p1: Coordinates = { x: 2, y: 1 };
    const p2: Coordinates = { x: 1, y: 1 };
    const p3 = getCoordinatesOfFollowingPointInDistanceToLastPointOnLine(p1, p2, 2);

    expect(p3.x).toBe(-1);
    expect(p3.y).toBe(1);
});
// Orientation Vertical -> Following point in  ∞ direction
test('should calculate correctly position of P3 if P1 and P2 are in I quadrant', () => {
    const p1: Coordinates = { x: 1, y: 1 };
    const p2: Coordinates = { x: 1, y: 2 };
    const p3 = getCoordinatesOfFollowingPointInDistanceToLastPointOnLine(p1, p2, 2);

    expect(p3.x).toBe(1);
    expect(p3.y).toBe(4);
});
// Orientation Vertical -> Following point in  ∞ direction
test('should calculate correctly position of P3 if P1 and P2 are in I quadrant', () => {
    const p1: Coordinates = { x: 1, y: 2 };
    const p2: Coordinates = { x: 1, y: 1 };
    const p3 = getCoordinatesOfFollowingPointInDistanceToLastPointOnLine(p1, p2, 2);

    expect(p3.x).toBe(1);
    expect(p3.y).toBe(-1);
});

I could add one if to detect this case but what if the line is under some tilt angle, then this will be very hard to decide how to calculate coordinates of the following point. So, the question is: How my algorithm should look like to make it work always?

Update 1

I have tried the algorithm linked by @Andreas How to find a third point given both (2 points on a line) and (distance from third point to first point), but it doesn't work for me unless I am doing something wrong. Below you can find how I implemented this:

function getCoordinatesOfFollowingPointInDistanceToLastPointOnLine (p1: Coordinates, p2: Coordinates,
    distance: number): Coordinates {
    const p1P2Distance = Math.sqrt((p2.x - p1.x) ** 2   (p2.y - p1.y) ** 2);
    const xDirectionLength = (p2.x - p1.x) / p1P2Distance;
    const yDirectionLength = (p2.y - p1.y) / p1P2Distance;
    const p3x = p1.x   distance * xDirectionLength;
    const p3y = p1.y   distance * yDirectionLength;

    return {
        x: Number(p3x.toFixed(3)),
        y: Number(p3y.toFixed(3))
    };
}

CodePudding user response：

The formula from the question I've mentioned in my comment works.
Your update calculates P3 from P1 (p1.x ..., p1.y ...) but it should be from P2

I've replaced your tests and objects with arrays, but the formula is the same.
I had to replace ** with the "old" Math.pow() because otherwise the fourth test would have failed because (p2.y - p1.y) ** 2 resulted in a NaN.

(~~ is used to get integers instead of floats)

const testCases = [
  /* P1, P2, distance, P3 */
    [[0, 1], [2, 1], 2, [ 4,  1]],
    [[2, 1], [1, 1], 2, [-1,  1]],
    [[1, 1], [1, 2], 2, [ 1,  4]],
    [[1, 2], [1, 1], 2, [ 1, -1]]
];

function getP3(p1, p2, distance) {
    const p1p2d = Math.sqrt(Math.pow(p2[0] - p1[0], 2)   Math.pow(p2[1] - p1[1], 2));
    const dx = (p2[0] - p1[0]) / p1p2d;
    const dy = (p2[1] - p1[1]) / p1p2d;
    const p3x = p2[0]   distance * dx;
    const p3y = p2[1]   distance * dy;

    return [~~p3x, ~~p3y];
}

testCases.forEach(({0: p1, 1: p2, 2: d, 3: e}) => {
  const p3 = getP3(p1, p2, d);
  console.log(p3, e, p3[0] == e[0], p3[1] == e[1]);
})