How to efficiently compute the future position of a point that will move in a box and bounce on its-CodePudding

I have a simple maths/physics problem here: In a Cartesian coordinate system, I have a point that moves in time with a known velocity. The point is inside a box, and bounces orthognally on its walls.

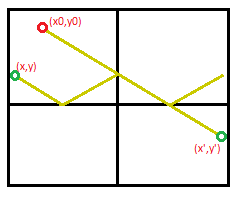
Here is a quick example I did on paint: example

What we know: The red point position, and its velocity which is defined by an angle θ and a speed. Of course we know the dimensions of the green box.

On the example, I've drawn in yellow its approximate trajectory, and let's say that after a determined period of time which is known, the red point is on the blue point. What would be the most efficient way to compute the blue point position?

I've tought about computing every "bounce point" with trigonometry and vector projection, but I feel like it's a waste of resources because trigonometric functions are usually very processor hungry. I'll have more than a thousand points to compute like that so I really need to find a more efficient way to do it.

If anyone has any idea, I'd be very grateful.

CodePudding user response：

Apart from programming considerations, it has an interesting solution from geometric point of view. You can find the position of the point at a specific time T without considering its temporal trajectory during 0<t<T

For one minute, forget the size and the boundaries of the box; and assume that the point can move on a straight line for ever. Then the point has constant velocity components vx = v*cos(θ), vy = v*sin(θ) and at time T its virtual porition will be x' = x0 vx * T, y' = y0 vy * T

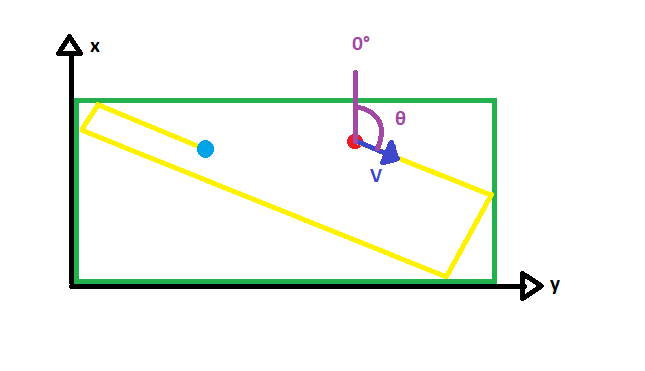
Now you need to map the virtual position (x',y') into the actual position (x,y). See image below

You can recursively reflect the virtual point w.r.t the borders until the point comes back into the reference (initial) box. And this is the actual point. Now the question is how to do these mathematics? and how to find (x,y) knowing (x',y')?

Denote by a and b the size of the box along x and y respectively. Then nx = floor(x'/a) and ny = floor(y'/b) indicates how far is the point from the reference box in terms of the number of boxes. Also dx = x'-nx*a and dy = y'-ny*b introduces the relative position of the virtual point inside its virtual box.

Now you can find the true position (x,y): if nx is even, then x = dx else x = a-dx; similarly if ny is even, then y = dy else y = b-dy. In other words, even number of reflections in each axis x and y, puts the true point and the virtual point in the same relative positions, while odd number of reflections make them different and complementary.

CodePudding user response：

You don't need to use trigonometric function all the time. Instead get normalized direction vector as (dx, dy) = (cos(θ), sin(θ))

After bouncing from vertical wall x-component changes it's sign dx = -dx, after bouncing from horizontal wall y-component changes it's sign dy = -dy. You can see that calculations are blazingly simple.

If you (by strange reason) prefer to use angles, use angle transformations from here (for ball with non-zero radius)

if ((ball.x   ball.radius) >= window.width || (ball.x - ball.radius) <= 0)
        ball.theta = M_PI - ball.theta;
  else
     if ((ball.y   ball.radius) >= window.height || (ball.y - ball.radius) <= 0) 
           ball.theta = - ball.theta;

To get point of bouncing:

Starting point (X0, Y0)
Ray angle Theta, c = Cos(Theta), s = Sin(Theta);
Rectangle coordinates: bottom left (X1,Y1), top right (X2,Y2)

if c >= 0 then //up
  XX = X2
else
  XX = X1

if s >= 0 then  //right
  YY = Y2
else
  YY = Y1

if c = 0 then //vertical ray
   return Intersection = (X0, YY)

if s = 0 then  //horizontal ray
   return Intersection = (XX, Y0)

tx = (XX - X0) / c   //parameter when vertical edge is met
ty = (YY - Y0) / s   //parameter when horizontal edge is met

if tx <= ty then  //vertical first
    return Intersection = (XX, Y0   tx * s)
else            //horizontal first
    return  Intersection = (X0   ty * c, YY)