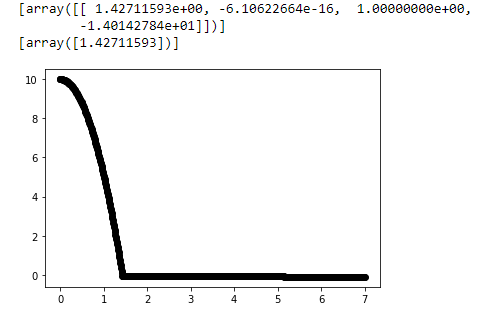
I want to solve ordinary differential equations using scipy_ivp() of a ball falling with an inital velocity of 1 in the x-direction, and 0 in the y-direction. The gravitational acceleration is g = 9.82, and when the ball hits the ground, its velocity is suppossed to change sign and be multiplied by 0.9. However, using the events parameter, I find it doesn't work as it should. This is my code and the result:

from scipy.integrate import solve_ivp
def f_derivs_ivp(t, vars, g = 9.82):
    
    dxdt = vars[2]
    dydt = vars[3]
    
    dvxdt = 0
    dvydt = -g
    
    return dxdt, dydt, dvxdt, dvydt

def bounce(t, y, g = 9.82):
    if y[1] <= 0:
        y[3] = -0.9*y[3]
    #print(y[1])
    return y[1]

#bounce.terminal = True
#bounce.direction = -1

vars0 = np.array([0, 10, 1, 0])

sol = solve_ivp(f_derivs_ivp, [0, 7], vars0, max_step=0.01, events = bounce)


plt.plot(sol.y[0], sol.y[1], "ko")

print(sol.y_events)
print(sol.t_events)

Using another method than scipy.ivp(), the result should look like this:

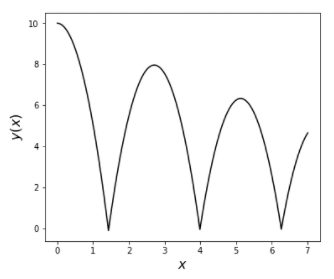
What am I doing wrong, and how does the events parameter work? Note also that if I write return y[1] - 10 in the bounce function, nothing changes. It bounces up and down if I in the if statement of the bounce function write y[3] = 10 for example, but not as it should.

CodePudding user response：

The scipy ODE solvers do not possess an event-action mechanism with user-definable actions. The event function is just a scalar-valued function on the trajectory whose zeros (with crossing-direction if set) are the events. This means that the event function is used to search for an event (first detecting sign changes, then refining using Brent's method). It will be called multiple times per time step independent on if the time step contains an event.

The built-in actions are "register" (default) and "terminate".

You will have to interrupt the integration at a bounce, and restart with the reflected state as initial condition. Plot the pieces separately or use concatenation to get one big solution array.