Test 80,000 simulated normal distribution observation sets against a null hypothesis-CodePudding

I need to generate a random sample of size 200 (n=200) from a normal distribution with variance 1 and true mu (average) I specify; then, I test the draw against a hypothesis: mu <= 1. I need to do this for each of 400 potential true thetas, and for each true theta I need to replicate this 200 times.

I already did this for n=1, but I realize my approach is not replicable. For each 400 thetas, I ran the following:

sample_r200n1_t2=normal(loc=-0.99, scale=1, size=200)
sample_r200n1_t3=normal(loc=-0.98, scale=1, size=200)
sample_r200n1_t4=normal(loc=-0.97, scale=1, size=200)
sample_r200n1_t5=normal(loc=-0.96, scale=1, size=200)
... on and on to loc = 3

Then, I tested each element in the generated array separately. However, that approach would require me to generate tens of thousands of samples, I generate the mean associated with each, then test that mean against my criteria. This would have to be done 80,000 times (and, on top of this I need to do this for multiple different sizes n). Clearly - this is not the approach to take.

How can I achieve the results I am looking for? Is there a way, for example, to generate an array of sample means and put those means into an array, one per theta? Then I could test as before. Or, is there another way?

CodePudding user response：

You can generate all 200*200*400 = 16 million random values in a numpy array (which consumes ~122 megabytes of memory; check with draws.nbytes/1024/1024), and use SciPy to run a one-sided, one-sample t-test on each of the 200 samples of 200 observations for each value of theta:

from numpy.random import normal
from scipy.stats import ttest_1samp
import matplotlib.pyplot as plt

# Array of loc values; for each loc, we draw 200 
# samples of 200 normally distributed observations
locs = np.linspace(-1, 3, 401)

# Array of shape (401, 200, 200) = (locs, samples, observations)
# Note that 200 draws of 200 i.i.d. observations is the same as
# 1 draw of 200*200 i.i.d. observations, reshaped to (200, 200)
draws = np.array([normal(loc=x, scale=1, size=200*200)
                  for x in locs]).reshape(401, 200, 200)

# axis=1 computes t-test across columns.
# Alternative hypothesis that sample mean
# is less than the population mean of 1 implies a null
# hypothesis that sample mean is greater than or equal to
# the population mean
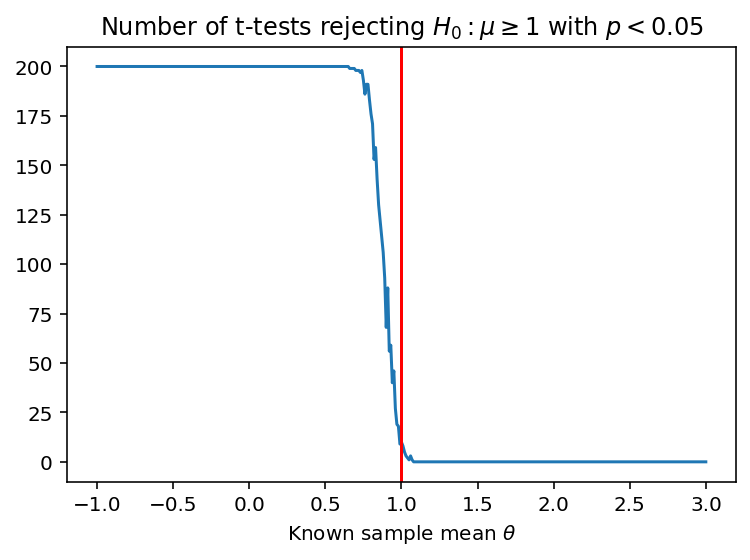
tstats, pvals = ttest_1samp(draws, 1, alternative='less', axis=1)

# Count how many out of 200 t-tests reject the null hypothesis
# at the alpha=0.05 level
rejects = (pvals < 0.05).sum(axis=1)

# Visual check: p-values should be low for sample means
# far below 1, as these tests should reject the null 
# hypothesis that sample mean >= 1
plt.plot(locs, rejects)
plt.axvline(1, c='r')
plt.title('Number of t-tests rejecting $H_0 : \mu \geq 1$ with $p < 0.05$')
plt.xlabel('Known sample mean $\\theta$')