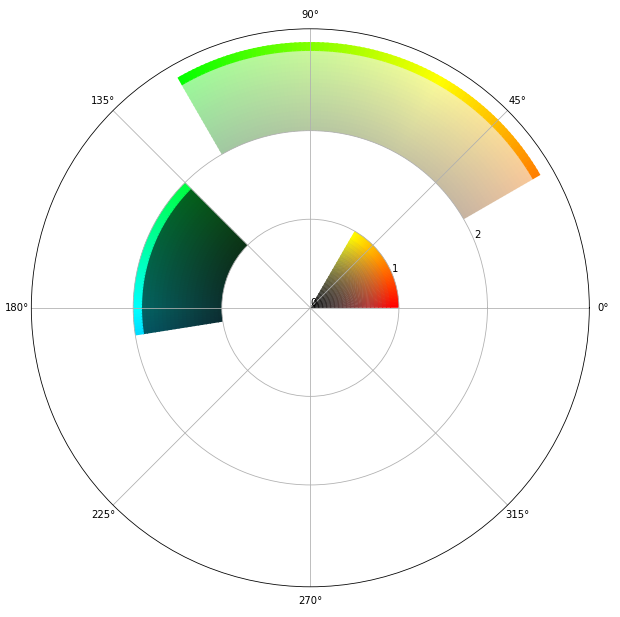
I am trying to generate a radial (circular) barplot displaying various color ranges in order to compare them. Using a radial barplot allows to better apprehend the circular nature of the hue value and to represent out-of-range ranges such as [340°, 10°]

To illustrate with this image, the idea is to replace the black color of the bars of the barplot on the left by the parts of the chromatic circle (displayed on the right) corresponding.

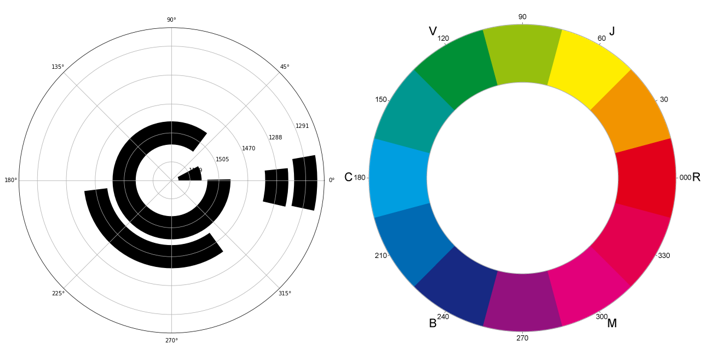
This is the code that I use to generate the radial barplot :

import matplotlib.pyplot as plt
from numpy import pi

start_values = [0, 3*pi/4, pi/6]
range_values = [pi/3, 3*pi/10, pi/2]

ax = plt.subplot(projection='polar')

for i in range(len(start_values)):
    ax.barh(i, range_values[i], left=start_values[i], color=(0, 0, 0))

I wanted to apply Matplotlib's hsv color map but the color parameter of barh() does not accept it.

On the internet I have only found techniques to apply gradients or cmaps to regular barplots, with rectangular bars (like this one: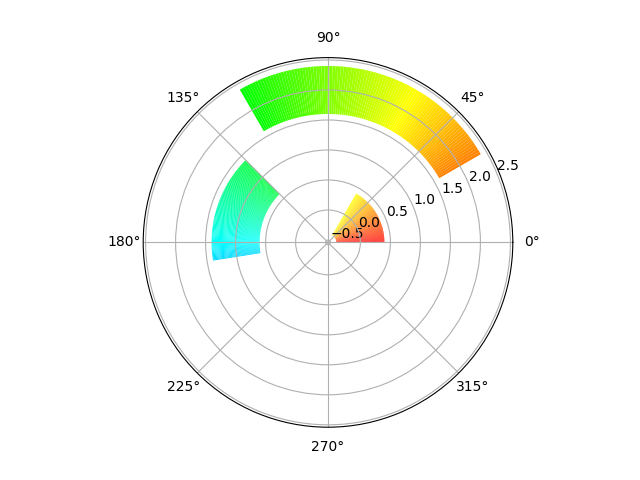

CodePudding user response：

Thanks Pierre, I used your technique to build a graph that also represents saturation and value as a gradient in the direction of the radius. Here is what it returns for the example given (with saturation and value ranges added)

Code:

figure, axes = plt.subplots(2, 2, figsize=(10, 20))

def radius_barplot(lower_color, upper_color, ax, index=None, angle_precision=1, hue_only=0.1):
    if index is None: index = range(len(lower_color[0]))
    ax = plt.subplot(projection='polar')
    pi2 = 2*pi
    full_color = 1 - hue_only

    for i, frame in enumerate(index):

        #print("Frame n°", i 1, sep='')
        min_hue, max_hue = lower_color[0][frame] / 179 * 2 * pi, upper_color[0][frame] / 179 * 2 * pi
        min_sat, min_val = lower_color[1][frame] / 255, lower_color[2][frame] / 255
        range_hue, range_sat, range_val = max_hue - min_hue, round(upper_color[1][frame] - lower_color[1][frame]), round(upper_color[2][frame] - lower_color[2][frame])
        n_height = min(max(range_sat, range_val), 20)
        pas_height = 1*full_color/n_height
        large_pas_angle, large_pas_height = angle_precision*1.5/180*pi, pas_height*1.25
        pas_sat, pas_val = range_sat / 255 / n_height, range_val / 255 / n_height

        #print("Angle range: [", round(min_hue/pi*180), "; ", round((max_hue)/pi*180), "]", sep='')
        
        # For each degree of the angle
        for angle in np.arange(min_hue, max_hue, angle_precision/180*pi):
            
            # To avoid an overflow on the end of the interval
            if angle   large_pas_angle > max_hue: large_pas_angle = max_hue - angle
                        
            # For each line inside the current bar
            for height in range(n_height):
                """
                print("Height: [", round(i   height*pas_height, 2), ", ", round(i   height*pas_height   pas_height, 2),
                      "], angle: ", round(angle/pi*180, 3),
                      "°: color [", round(angle*360), ", ", round((min_sat   height*pas_sat)*100), ", ", round((min_val   height*pas_val)*100), "]", sep='')
                """
                ax.barh(y=i   height*pas_height,
                        width=large_pas_angle, left=angle, height=large_pas_height, align='edge',
                        color=colorsys.hsv_to_rgb(angle/pi2,
                                                  min_sat   height*pas_sat,
                                                  min_val   height*pas_val)
                        )
            
            # To display the reference hue (with full saturation and value)
            ax.barh(y=i   full_color,
                    width=large_pas_angle, left=angle, height=hue_only, align='edge',
                    color=colorsys.hsv_to_rgb(angle/pi2, 1, 1)
                    )
            # """
        ax.set_rgrids(range(len(index)), labels=index)

# Execute the function with the example data
radius_barplot(
    ((0, (3*pi/4)/(2*pi)*179, (pi/6)/(2*pi)*179), (0, 200, 50), (0, 50, 200)),  # Minimal values of colors ranges
    (((pi/3)/(2*pi)*179, (21*pi/20)/(2*pi)*179, (2*pi/3)/(2*pi)*179), (255, 250, 100), (255, 100, 250)),  # Maximal values of colors ranges
               axes[0])

Graph:

The main problem of this technique is its complexity: returning this graph took 1 minute and 45 seconds on my computer and getting the graph I am interested in takes almost 5 minutes.

So if someone has a better, more optimal method to obtain a similar result I would still be interested.