Neural network back propagation regression, how to correctly learn the cos function?-CodePudding

I found that it may be a problem with PyCharm's cache. After I learned the sin function, I changed sin directly to cos and ran it without saving. The 2000th time was still the wrong result.

Epoch:0/2001 Error:0.2798077795267396
Epoch: 200/2001 Error: 0.27165245260858123
Epoch: 400/2001 Error: 0.2778566883056528
Epoch: 600/2001 Error: 0.26485675644837514
Epoch: 800/2001 Error: 0.2752758904739536
Epoch: 1000/2001 Error: 0.2633888652172328
Epoch: 1200/2001 Error: 0.2627593240503436
Epoch: 1400/2001 Error: 0.27195552955032104
Epoch: 1600/2001 Error: 0.27268507931720914
Epoch: 1800/2001 Error: 0.2689462168186385
Epoch: 2000/2001 Error: 0.2737487268797401

The 2000th results are as follows: 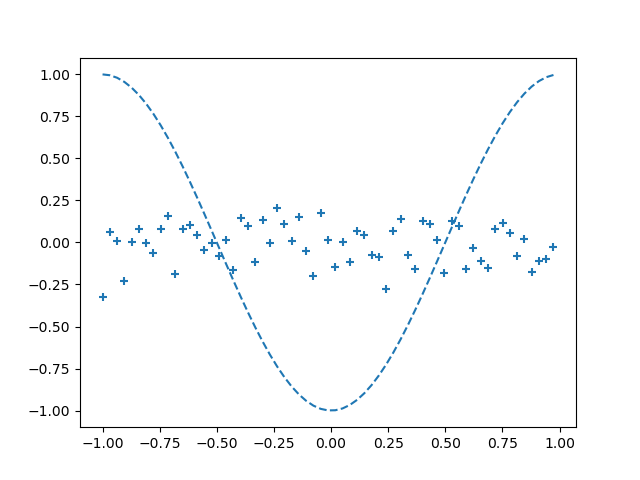But if I save and use "Reload all from disk", the error of the 400th time is already very small.

Epoch:0/2001 Error:0.274032588963002
Epoch: 200/2001 Error: 0.2718715689675884
Epoch: 400/2001 Error: 0.0014035324029329518
Epoch:600/2001 Error:0.0004188502356206808
Epoch: 800/2001 Error: 0.000202233202030069
Epoch: 1000/2001 Error: 0.00014405423567078488
Epoch: 1200/2001 Error: 0.00011676179819916471
Epoch: 1400/2001 Error: 0.00011185491417278027
Epoch: 1600/2001 Error: 0.000105762467718704
Epoch:1800/2001 Error:8.768434766422346e-05
Epoch: 2000/2001 Error: 9.686019331806035e-05

The 400th results are as follows:

I use neural network back propagation regression to learn the cos function. When I learn the sin function, it is normal. If it is changed to cos, it is abnormal. What is the problem?

correct_data = np.cos(input_data)

Related settings:

1.The activation function of the middle layer: sigmoid function

2.Excitation function of the output layer: identity function

3.Loss function: sum of squares error

4.Optimization algorithm: stochastic gradient descent method

5.Batch size: 1

My code is as follows:

import numpy as np
import matplotlib.pyplot as plt

# - Prepare to input and correct answer data -
input_data = np.arange(0, np.pi * 2, 0.1)  # input
correct_data = np.cos(input_data)  # correct answer
input_data = (input_data - np.pi) / np.pi  # Converge the input to the range of -1.0-1.0
n_data = len(correct_data)  # number of data

# - Each setting value -
n_in = 1  # The number of neurons in the input layer
n_mid = 3  # The number of neurons in the middle layer
n_out = 1  # The number of neurons in the output layer

wb_width = 0.01  # The spread of weights and biases
eta = 0.1  # learning coefficient
epoch = 2001
interval = 200  # Display progress interval practice


# -- middle layer --
class MiddleLayer:
    def __init__(self, n_upper, n):  # Initialize settings
        self.w = wb_width * np.random.randn(n_upper, n)  # weight (matrix)
        self.b = wb_width * np.random.randn(n)  # offset (vector)

    def forward(self, x):  # forward propagation
        self.x = x
        u = np.dot(x, self.w)   self.b
        self.y = 1 / (1   np.exp(-u))  # Sigmoid function

    def backward(self, grad_y):  # Backpropagation
        delta = grad_y * (1 - self.y) * self.y  # Differentiation of Sigmoid function

        self.grad_w = np.dot(self.x.T, delta)
        self.grad_b = np.sum(delta, axis=0)

        self.grad_x = np.dot(delta, self.w.T)

    def update(self, eta):  # update of weight and bias
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b


# - Output layer -
class OutputLayer:
    def __init__(self, n_upper, n):  # Initialize settings
        self.w = wb_width * np.random.randn(n_upper, n)  # weight (matrix)
        self.b = wb_width * np.random.randn(n)  # offset (vector)

    def forward(self, x):  # forward propagation
        self.x = x
        u = np.dot(x, self.w)   self.b
        self.y = u  # Identity function

    def backward(self, t):  # Backpropagation
        delta = self.y - t

        self.grad_w = np.dot(self.x.T, delta)
        self.grad_b = np.sum(delta, axis=0)

        self.grad_x = np.dot(delta, self.w.T)

    def update(self, eta):  # update of weight and bias
        self.w -= eta * self.grad_w
        self.b -= eta * self.grad_b


# - Initialization of each network layer -
middle_layer = MiddleLayer(n_in, n_mid)
output_layer = OutputLayer(n_mid, n_out)

# -- learn --
for i in range(epoch):

    # Randomly scramble the index value
    index_random = np.arange(n_data)
    np.random.shuffle(index_random)

    # Used for the display of results
    total_error = 0
    plot_x = []
    plot_y = []

    for idx in index_random:

        x = input_data[idx:idx   1]  # input
        t = correct_data[idx:idx   1]  # correct answer

        # Forward spread
        middle_layer.forward(x.reshape(1, 1))  # Convert the input to a matrix
        output_layer.forward(middle_layer.y)

        # Backpropagation
        output_layer.backward(t.reshape(1, 1))  # Convert the correct answer to a matrix
        middle_layer.backward(output_layer.grad_x)

        # Update of weights and biases
        middle_layer.update(eta)
        output_layer.update(eta)

        if i % interval == 0:
            y = output_layer.y.reshape(-1)  # Restore the matrix to a vector

            # Error calculation
            total_error  = 1.0 / 2.0 * np.sum(np.square(y - t))  # Square sum error

            # Output record
            plot_x.append(x)
            plot_y.append(y)

    if i % interval == 0:
        # Display the output with a graph
        plt.plot(input_data, correct_data, linestyle="dashed")
        plt.scatter(plot_x, plot_y, marker=" ")
        plt.show()

        # Display the number of epochs and errors
        print("Epoch:"   str(i)   "/"   str(epoch), "Error:"   str(total_error / n_data))

CodePudding user response：

If increasing the number of epochs worked, the model needed more training.

But you may be overfitting... Notice that the cosine function is a periodic function, yet you are using only monotonic functions (sigmoid, and identity) to approximate it.

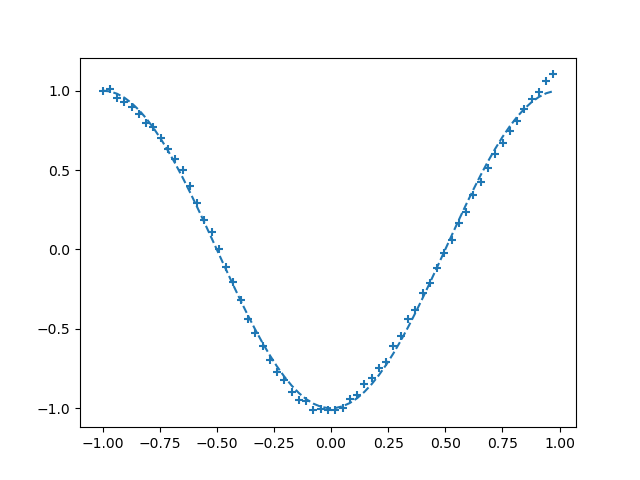
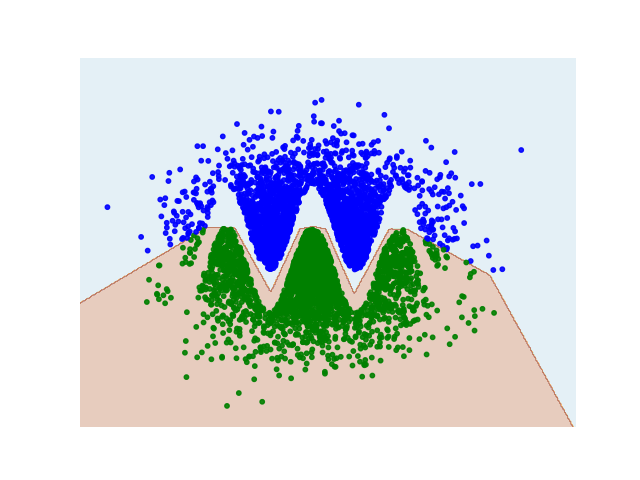
So while on the bounded interval of your data it may work:

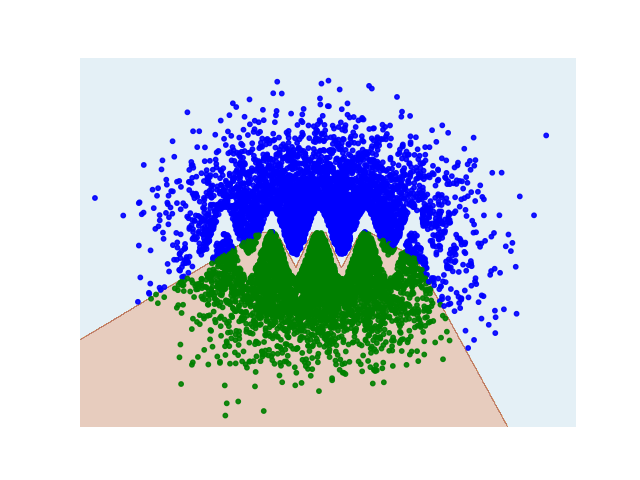
It does not generalize well: