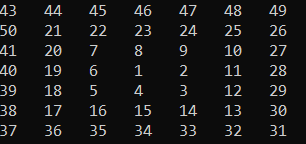
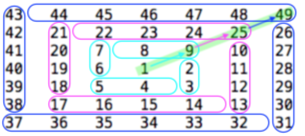
I recently finished making an algorithm for a project I'm working on.
Briefly, a part of my project needs to fill a matrix, the requirements of how to do it are these:
- Fill the matrix in form of spiral, from the center.
- The size of the matrix must be dynamic, so the spiral can be large or small.
- Every two times a cell of the matrix is filled, //DO STUFF must be executed.
In the end, the code that I made works, it was my best effort and I am not able to optimize it more, it bothers me a bit having had to use so many ifs, and I was wondering if someone could take a look at my code to see if it is possible to optimize it further or some constructive comment (it works well, but it would be great if it was faster, since this algorithm will be executed several times in my project). Also so that other people can use it!
#include <stdio.h>
typedef unsigned short u16_t;
const u16_t size = 7; //<-- CHANGE HERE!!! just odd numbers and bigger than 3
const u16_t maxTimes = 2;
u16_t array_cont[size][size] = { 0 };
u16_t counter = 3, curr = 0;
u16_t endColumn = (size - 1) / 2, endRow = endColumn;
u16_t startColumn = endColumn 1, startRow = endColumn 1;
u16_t posLoop = 2, buffer = startColumn, i = 0;
void fillArray() {
if (curr < maxTimes) {
if (posLoop == 0) { //Top
for (i = buffer; i <= startColumn && curr < maxTimes; i , curr )
array_cont[endRow][i] = counter ;
if (curr == maxTimes) {
if (i <= startColumn) {
buffer = i;
} else {
buffer = endRow;
startColumn ;
posLoop ;
}
} else {
buffer = endRow;
startColumn ;
posLoop ;
fillArray();
}
} else if (posLoop == 1) { //Right
for (i = buffer; i <= startRow && curr < maxTimes; i , curr )
array_cont[i][startColumn] = counter ;
if (curr == maxTimes) {
if (i <= startRow) {
buffer = i;
} else {
buffer = startColumn;
startRow ;
posLoop ;
}
} else {
buffer = startColumn;
startRow ;
posLoop ;
fillArray();
}
} else if (posLoop == 2) { //Bottom
for (i = buffer; i >= endColumn && curr < maxTimes; i--, curr )
array_cont[startRow][i] = counter ;
if (curr == maxTimes) {
if (i >= endColumn) {
buffer = i;
} else {
buffer = startRow;
endColumn--;
posLoop ;
}
} else {
buffer = startRow;
endColumn--;
posLoop ;
fillArray();
}
} else if (posLoop == 3) { //Left
for (i = buffer; i >= endRow && curr < maxTimes; i--, curr )
array_cont[i][endColumn] = counter ;
if (curr == maxTimes) {
if (i >= endRow) {
buffer = i;
} else {
buffer = endColumn;
endRow--;
posLoop = 0;
}
} else {
buffer = endColumn;
endRow--;
posLoop = 0;
fillArray();
}
}
}
}
int main(void) {
array_cont[endColumn][endColumn] = 1;
array_cont[endColumn][endColumn 1] = 2;
//DO STUFF
u16_t max = ((size * size) - 1) / maxTimes;
for (u16_t j = 0; j < max; j ) {
fillArray();
curr = 0;
//DO STUFF
}
//Demostration
for (u16_t x = 0; x < size; x ) {
for (u16_t y = 0; y < size; y )
printf("%-4d ", array_cont[x][y]);
printf("\n");
}
return 0;
}
CodePudding user response:
Notice that the numbers along the diagonal (1, 9, 25, 49) are the squares of the odd numbers. That's an important clue, since it suggests that the 1 in the center of the matrix should be treated as the end of a spiral.
From the end of each spiral, the x,y coordinates should be adjusted up and to the right by 1. Then the next layer of the spiral can be constructed by moving down, left, up, and right by the same amount.
For example, starting from the position of the 1, move up and to the right (to the position of the 9), and then form a loop with the following procedure:
move down, and place the 2
move down, and place the 3
move left, and place the 4
move left, and place the 5
etc.
Thus the code looks something like this:
int size = 7;
int matrix[size][size];
int dy[] = { 1, 0, -1, 0 };
int dx[] = { 0, -1, 0, 1 };
int directionCount = 4;
int ringCount = (size - 1) / 2;
int y = ringCount;
int x = ringCount;
int repeatCount = 0;
int value = 1;
matrix[y][x] = value ;
for (int ring = 0; ring < ringCount; ring )
{
y--;
x ;
repeatCount = 2;
for (int direction = 0; direction < directionCount; direction )
for (int repeat = 0; repeat < repeatCount; repeat )
{
y = dy[direction];
x = dx[direction];
matrix[y][x] = value ;
}
}
CodePudding user response:
I saw already many approaches for doing a spiral. All a basically drawing it, by following a path.
BUT, you can also come up with an analytical calculation formula for a spiral.
So, no recursion or iterative solution by following a path or such. We can directly calculate the indices in the matrix, if we have the running number.
I will start with the spiral in mathematical positive direction (counter clockwise) in a cartesian coordinate system. We will concentrate on X and Y coordinates.
I made a short Excel and derived some formulas from that. Here is a short picture:
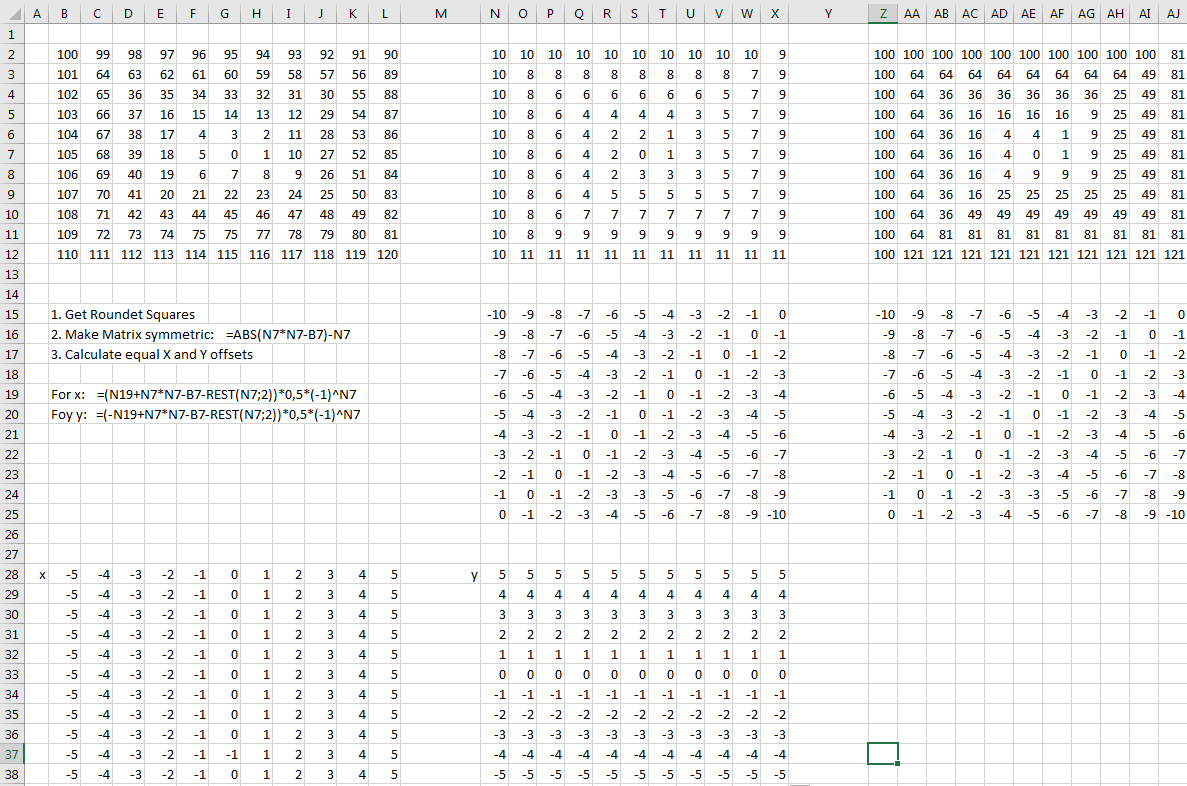
From the requirements we know that the matrix will be quadratic. That makes things easier. A little bit trickier is, to get the matrix data symmetrical. But with some simple formulas, derived from the prictures, this is not really a problem.
And then we can calculate x and y coordinates with some simple statements. See the below example program with long variable names for better understanding. The code is made using some step by step approach to illustrate the implementation. Of course it can be made more compact easily. Anyway. Let's have a look.
#include <iostream>
#include <cmath>
#include <iomanip>
int main() {
// Show some example values
for (long step{}; step < 81; step) {
// Calculate result
const long roundedSquareRoot = std::lround(std::sqrt(step));
const long roundedSquare = roundedSquareRoot * roundedSquareRoot;
const long distance = std::abs(roundedSquare - step) - roundedSquareRoot;
const long rsrIsOdd = (roundedSquareRoot % 2);
const long x = (distance roundedSquare - step - rsrIsOdd) / (rsrIsOdd ? -2 : 2);
const long y = (-distance roundedSquare - step - rsrIsOdd) / (rsrIsOdd ? -2 : 2);
// Show ouput
std::cout << "Step:" << std::setw(4) << step << std::setw(3) << x << ' ' << std::setw(3) << y << '\n';
}
}
So, you see that we really have an analytical solution. Given any number we can calculate the x and y coordinate using a formula. Cool.
Getting indices in a matrix is just adding some offset.
With that gained know how, we can now easily calculate the complete matrix. And, since there is no runtime activity needed at all, we can let the compiler do the work. We will simply use constexpr functions for everything.
Then the compiler will create this matrix at compile time. At runtime, nothing will happen.
Please see a very compact solution:
#include <iostream>
#include <iomanip>
#include <array>
constexpr size_t MatrixSize = 15u;
using MyType = long;
static_assert(MatrixSize > 0 && MatrixSize%2, "Matrix size must be odd and > 0");
constexpr MyType MatrixHalf = MatrixSize / 2;
using Matrix = std::array<std::array<MyType, MatrixSize>, MatrixSize >;
// Some constexpr simple mathematical functions ------------------------------------------------------------------------------
// No need for <cmath>
constexpr MyType myAbs(MyType v) { return v < 0 ? -v : v; }
constexpr double mySqrtRecursive(double x, double c, double p) {return c == p? c: mySqrtRecursive(x, 0.5 * (c x / c), c); }
constexpr MyType mySqrt(MyType x) {return (MyType)(mySqrtRecursive((double)x,(double)x,0.0) 0.5); }
// Main constexpr function will fill the matrix with a spiral pattern during compile time -------------------------------------
constexpr Matrix fillMatrix() {
Matrix matrix{};
for (int i{}; i < (MatrixSize * MatrixSize); i) {
const MyType rsr{ mySqrt(i) }, rs{ rsr * rsr }, d{ myAbs(rs - i) - rsr }, o{ rsr % 2 };
const size_t col{ (size_t)(MatrixHalf ((d rs - i - o) / (o ? -2 : 2)))};
const size_t row{ (size_t)(MatrixHalf -((-d rs - i - o) / (o ? -2 : 2)))};
matrix[row][col] = i;
}
return matrix;
}
// This is a compile time constant!
constexpr Matrix matrix = fillMatrix();
// All the above has been done during compile time! -----------------------------------------
int main() {
// Nothing to do. All has beend done at compile time already!
// The matrix is already filled with a spiral pattern
// Just output
for (const auto& row : matrix) {
for (const auto& col : row) std::cout << std::setw(5) << col << ' '; std::cout << '\n';
}
}
Different coordinate systems or other spiral direction can be adapted easily.
Happy coding.