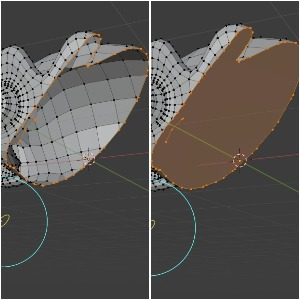
I'm trying to write an algorithm for cutting tessellated mesh with the given plane (plane defined with the point on the plane and unit normal vector). Also, this algorithm should triangulate all polygons and fill the hole after split. I faced with a problem to find a polygon that lies on the plane (like the orange plane on the image)

I tried to process all edges of all triangles and find those that lies on the plane and stored them in an array. After that, I formed an array of vertices by searching next suitable edge.

Can someone explain an easier and faster way to find this polygon?
All vertices must be stored in CCW order.

CodePudding user response：

Identify all edges that you cut by the indexes (or labels) of the endpoints. Make sure that every edge belongs to exactly two faces and is cut twice. Also make sure to orient the edge that results from the intersection consistently with the direction of the face normal.

Now the intersection edges form a chain that you can reconstruct by sorting: store the indexes of the endpoints separately, each with a link to the originating edge. After sorting on the indexes, the common vertices will appear in pairs in the sorted array. Using this structure, you can trace the polygon(s).

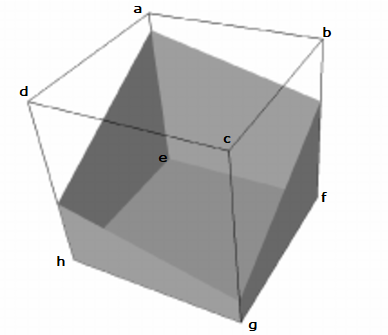
In the example below, from the faces aebf, bcgf, cdgh and dhea, you generate the edges ae-dh, bf-ae, cg-bf and dh-cg in some order. After splitting the endpoints and sorting, ae-, -ae, dh-, -dh, cg-, -cg, bf-, -bf, which generate the cycle ae-dh, dh-cg, cg-bf, bf-ae.