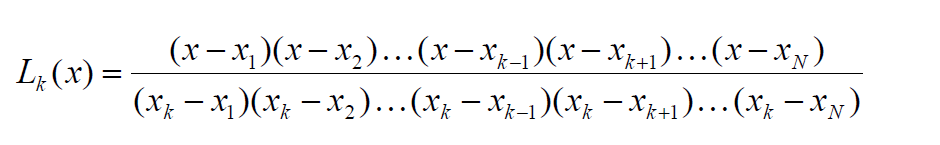Finding a quicker method to construct a matrix in python-CodePudding

I'm trying to construct a (p 1,n) matrix with the code below:

import numpy as np

p = 3
xh = np.linspace(0.5,1.5,p 1)
n = 7
x = np.linspace(0,2,n)

M = np.zeros([p 1,n])
l2 = 1

for i in range(len(x)):
    for k in range(len(xh)):
        for j in range(len(xh)):
            if k != j:
                l = (x[i]-xh[j])/(xh[k]-xh[j])
                l2 *= l
            elif k == j:
                l = 1
                l2 *= l
        M[k][i]=l2
        l2 = 1 
print(M)

This method produces the matrix I want but is very slow (6 sec for p=40 and n=2000).

The matrix itself is a matrix of lagrange polynomials, for approximating some function. The nodal points, xh, are the points used in forming/calculating the interpolation of a function. They have the property that their values on the original function and the interpolation are always the same. The number of distinct nodal points (p 1) indicate the degree (p) of the polynomial for the Lagrange interpolation. The x points are where a function is to be evaluated. That could be the interpolation of the function or the function. This is the formula I'm following:

I don't know how a faster way to construct a matrix in numpy, other methods seem to keep going wrong when I apply it to the code I've got and I don't know enough to see why. What faster method can I use here?

CodePudding user response：

Your code can be nicely compiled by decorating a function with @nb.njit from the numba package. Some minor redundant parts were removed.

import numpy as np
import numba as nb

@nb.njit
def test(p,n):
    xh = np.linspace(0.5,1.5,p 1)
    x = np.linspace(0,2,n)
    M = np.zeros((p 1,n), dtype=nb.float64)
    l2 = 1

    for k in range(len(x)):
        for i in range(len(xh)):
            for j in range(len(xh)):
                if i != j:
                    l = (x[k]-xh[j])/(xh[i]-xh[j])
                else:
                    l = 1
                l2 *= l
            M[i][k]=l2
            l2 = 1 
    return M

Benchmark for p=40, n=2000 on a 2-core colab instance. Array M was computed with your original code.

a = [0]
%timeit a[0] = test(40,2000)
np.testing.assert_allclose(M, a[0])

Runs in 5.57 ms per loop vs 2.24 s per loop or ~402x speed up.