Array max consecutive sum of k possible elements-CodePudding

Given array of integers, find the maximal possible sum of some of its k consecutive elements.
Example

For inputArray = [2, 3, 5, 1, 6]
and k = 2, the output should be solution(inputArray, k) = 8.

So my program kind of works, at least the test cases that I have seen, except for the fact that it skips the first element.

There are probably multiple ways of solving it. Either by inserting a copy of the first element to the array or make a seperate loop that loops through the first check (2 3 = 5). But none of these solutions really seem to be elegant enough. I want to solve this the best possible way and I cant seem to a good solution. This is my code:

vector<int> arr = {1, 3, 4, 2, 4, 19, 1};
    int sum {};
    int max {};
    int k = 3;

for (int i {}; i < arr.size();   i)
{
    sum = 0;
    int x = k;

    for (int j = i 1; j < arr.size();   j)
    {
        sum  = arr.at(j);
        --x;
        
        if (x == 0)
        {
            cout << sum << endl;
            break;
        }
    }
    
    if (sum > max)
    {
        max = sum;
    }
}

cout << max << endl;

As you can see my inner for loop starts with the index j 1 so it skips the first index in the vector by default. How do I fix this? Is there an if-statement I can do to manipulate the loop to only have j = i 1 if i != 0?

CodePudding user response：

Is there an if-statement I can do to manipulate the loop to only have j = i 1 if i != 0?

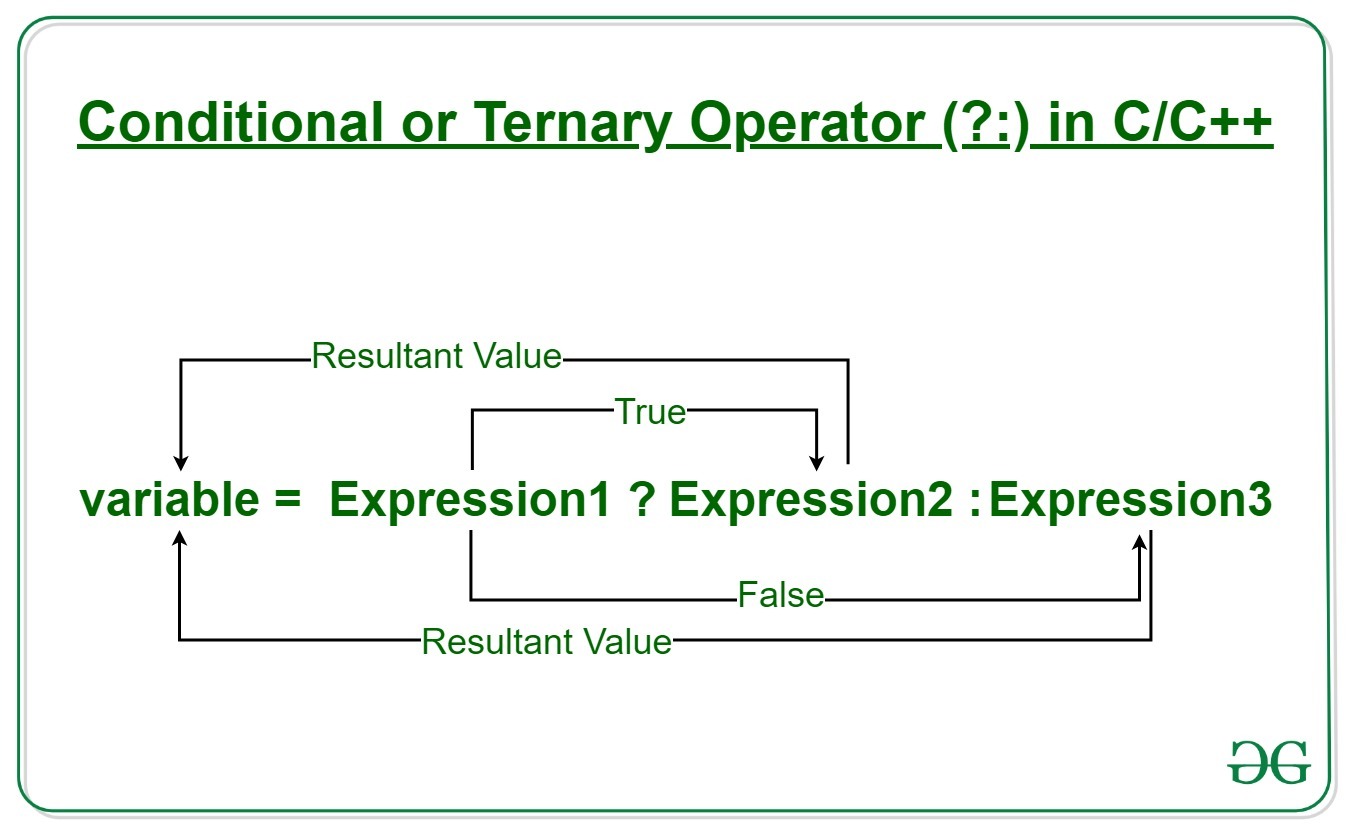
You can use a ternary operator to do it, something like that:

int j = i != 0 ? i   1 : i;

Structure of a ternary operator:

But, I got curious: why you don't add the value i to the sum (so it's always part of the sum), instead of starting it with zero?

sum = array[i];

CodePudding user response：

There are probably multiple ways of solving it. [...] I want to solve this the best possible way.

Then, consider a O(N) algorithm, instead of a O(N^2) one:

#include <iostream>
#include <vector>

auto max_sum_of_k(std::vector<int> const& v, size_t k)
{
  // Sum the first k elements.
  long long current_sum{};
  size_t i{};
  for ( ; i < k and i < v.size();   i )
  {
    current_sum  = v[i];
  }
  
  // Update the running sum, without a nested loop. 
  long long sum{ current_sum };
  for ( ; i < v.size();   i )
  {
    current_sum -= v[i - k];
    current_sum  = v[i];
    if ( sum < current_sum )
      sum = current_sum;
  }
  return sum;
}

int main()
{
  std::vector<int> arr = {1, 3, 4, 2, 4, 19, 1};

  for (size_t k{}; k <= arr.size();   k)
  {
      std::cout << "k: " << k << "  max sum: " << max_sum_of_k(arr, k) << '\n';
  }
}

CodePudding user response：

First note that this task is only possible if k does not exceed the array length.

Now an efficient solution is to

compute the sum of the first k elements, then
repeatedly remove the first element from the sum and add the next one. This makes a significant saving.

int j;
int Sum= A[0];
for (j= 1; j < k; j  )
  Sum = A[j];

// Here we have the first sum

for ( ; j < length; j  )
{
  Sum-= A[j - k];
  Sum = A[j];

  // Here we have the next sums
}

I leave you as an exercise to keep the maximum sum.

Notice that the sum update trick is not recommended for floating-point types, due to the accumulation of numerical errors.

CodePudding user response：

A bit fancy way to do it, using templates:

template <typename In>
auto sum_at_most_n(In b, In e, size_t n) {
    typename std::iterator_traits<In>::value_type sum{};
    while (b != e && n--) {
        sum = sum   *b  ;
    }
    return std::pair{sum, b};
}

template <typename In>
auto max_sum_of_k(In b, In e, size_t k) {
    auto [sum, head] = sum_at_most_n(b, e, k);
    auto max_sum = sum;
    while (head != e) {
        sum = sum - *b     *head  ;
        max_sum = std::max(max_sum, sum);
    }
    return max_sum;
}

template <typename Container>
auto max_sum_of_k(Container c, size_t k) ->
    typename std::iterator_traits<decltype(std::begin(c))>::value_type {
    return max_sum_of_k(std::begin(c), std::end(c), k);
}

Just iterating over elements and then subtraction elements which are no longer part of the sum,
but I really recommend to learn how to write tests. See link with demo:

Demo