I get this question in the Java notes and I see people solve it differently (with different answers too) can anyone please explain to me how we go about solving such questions?

• Suppose we analyze algorithm A to determine its time complexity and we determine that f(n) = 137.5n³ 2125.25n² 15033n 31595. If we let g(n) = n³ and C be 138 then what would the minimum integer value of the constant n0 have to be in order to prove that the time complexity of A is O(n³)?

CodePudding user response：

You need to solve

P(n):= 137.5n³   2125.25n²   15033n   31595 - 138n³ ≤ 0

but any higher value of n will do. The ratio of the quadratic and cubic coefficients is 4250.5, so probably n0 = 5000 will do. After checking, it does.

To find the smallest value, you can fortunately avoid solving the cubic. Indeed, given the order of magnitude of n0, the constant term is negligible and you can solve the quadratic inequation

- 0.5n²   2125.25n   15033 ≤ 0

which gives the largest root 2457.56...

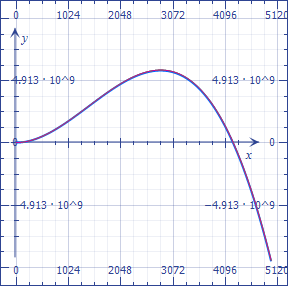
Now you can confirm that P(4257) > 0 while P(4258) < 0. You could also have worked this out by exhaustive search starting from n = 4251.

Below, the curves show that the approximations of P by dropping the last or last two terms are virtually undistinguishable from the full function.

Final remark:

For n > 1,

137.5   2125.25/n   15033/n²   31595/n³ < 48890.75

so that

137.5n³   2125.25n²   15033n   31595 < 48890.75n³

which proves O(N³) even more easily.