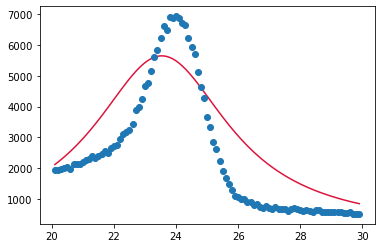
Here is the data I used for the fit which does not work:

x_vals = [20.1 20.2 20.3 20.4 20.5 20.6 20.7 20.8 20.9 21.  21.1 21.2 21.3 21.4
 21.5 21.6 21.7 21.8 21.9 22.  22.1 22.2 22.3 22.4 22.5 22.6 22.7 22.8
 22.9 23.  23.1 23.2 23.3 23.4 23.5 23.6 23.7 23.8 23.9 24.  24.1 24.2
 24.3 24.4 24.5 24.6 24.7 24.8 24.9 25.  25.1 25.2 25.3 25.4 25.5 25.6
 25.7 25.8 25.9 26.  26.1 26.2 26.3 26.4 26.5 26.6 26.7 26.8 26.9 27.
 27.1 27.2 27.3 27.4 27.5 27.6 27.7 27.8 27.9 28.  28.1 28.2 28.3 28.4
 28.5 28.6 28.7 28.8 28.9 29.  29.1 29.2 29.3 29.4 29.5 29.6 29.7 29.8
 29.9]

y_vals = [1922 1947 1985 2019 2050 1955 2143 2133 2132 2214 2268 2293 2397 2339
 2407 2447 2540 2504 2661 2714 2758 2945 3108 3161 3254 3434 3883 3997
 4250 4659 4782 5150 5603 5833 6225 6613 6502 6911 6873 6941 6876 6709
 6663 6238 5949 5728 5120 4649 4273 3671 3340 2855 2621 2246 1920 1666
 1476 1293 1099 1061  982  993  908  905  806  821  744  705  751  701
  673  728  662  677  658  615  684  688  679  624  600  622  608  572
  626  637  586  567  579  576  572  585  557  536  549  565  509  511
  521]

The fit isn't so great, its off by a lot and I am not sure how to fix it. Please let me know if there is a better way to fit this.

def lorentzian(x, a, x0):
    return a / ((x-x0)**2   a**2) / np.pi

# Obtain xdata and ydata
...

# Initial guess of the parameters (you must find them some way!)
#pguess = [2.6, 24]

# Fit the data
normalization_factor = np.trapz(x_vals, y_vals)  # area under the curve

popt, pcov = curve_fit(lorentzian, x_vals, y_vals/normalization_factor)

# Results
a, x0 = popt[0], popt[1]


plt.plot(x_vals, lorentzian(x_vals, popt[0], popt[1])*(normalization_factor),
           color='crimson', label='Fitted function')

plt.plot(x_vals, y_vals, 'o', label='data')


plt.show()

CodePudding user response：

You have the arguments to np.trapz reversed. It should be

normalization_factor = np.trapz(y_vals, x_vals)