Power series with array input-CodePudding

I want to do the following in Matlab:

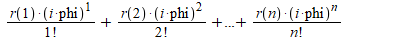
equation

i is the imaginary unit

r is a vector of length n: [r(1),...,r(n)]

phi is a 1x300 double, i.e. [phi(1),...,phi(300)]

sum(r(1:n).*(1i.^(1:n))./factorial(1:n))

This would work if there was no phi. But how can I implement the phi here?

sum(r(1:n).*((phi*1i).^(1:n))./factorial(1:n))

results in:

Matrix dimensions must agree.

The expected output is the same size as phi. This code would achieve what I want but I want n to be dynamic so the looping is not feasible:

if n==1
    R = r(1) * ( i * phi )
elseif n==2
    R = r(1) * ( i * phi )   r(2) * ( i * phi ).^2 / 2;
elseif n==3
    R = r(1) * ( i * phi )   r(2) * ( i * phi ).^2 / 2   r(3) * ( i * phi ).^3 / 6;
...

CodePudding user response：

You need to transpose phi, and then transpose your result back at the end, this looks something like

s = sum(r(1:n).*((phi.'*1i).^(1:n))./factorial(1:n),2).'

note the .' after phi and at the end to transpose. I've also included ,2 in the sum to sum along the 2nd dimension.

This relies on implicit expansion to create an intermediate matrix.

i.e. the operations between phi.' (a column array) and your row arrays (r(1:n), (1:n), and factorial(1:n)) are evaluated element-wise, making a matrix which is 300 x n. Then we sum in the 2nd dimension (sum(__,2)) to get a 300x1 output, which is finally transposed back to a 1x300 output to match your original phi.

CodePudding user response：

Given your example, you could do

ind_end = min(n, length(phi))
sum(r(1:ind_end).*((phi(1:ind_end)*1i).^(1:ind_end))./factorial(1:ind_end))

This works for any n by avoiding the indexing to go beyond the length of phi.