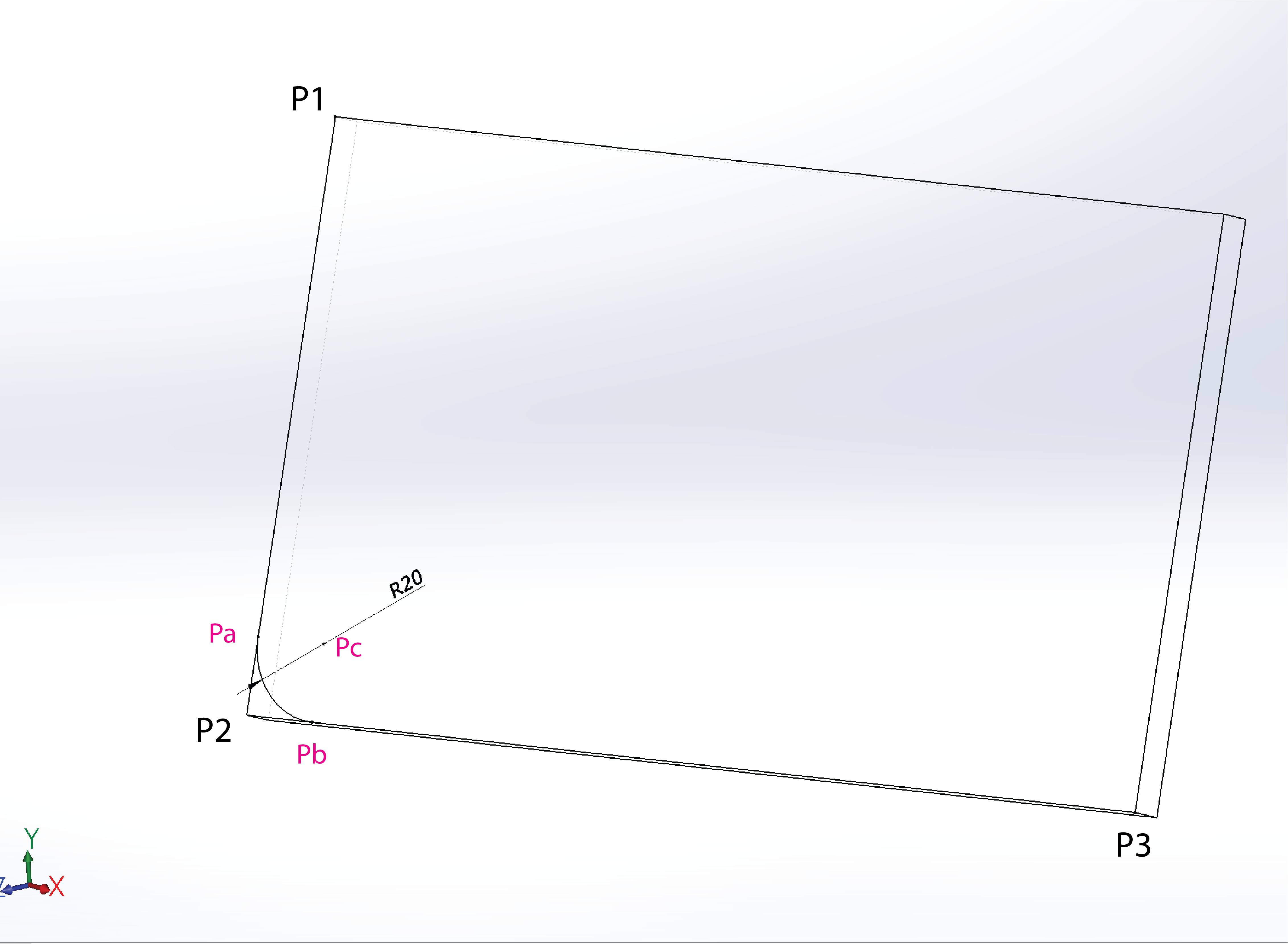
How can i add an arc where two 3D lines meet?

Known: Radius, P1, P2, P3.

what i need: Pa (arc start point3D), Pb (arc end Point3D), Pc (arc center point3D),

        double radius = 20;
        Vector3D P1 = new Vector3D(341.21, 227.208, 193.38);
        Vector3D P2 = new Vector3D(360.78, 85.34, 245.723);
        Vector3D P3 = new Vector3D(614.64, 85.34, 150.80);

        Vector3D P2P1 = new Vector3D(); 
        P2P1 = P1 - P2;


        Vector3D P2P3 = new Vector3D();
        P2P3 = P3 - P2;

I have found this answer on math.stackexchange, but i don't know all math symbols

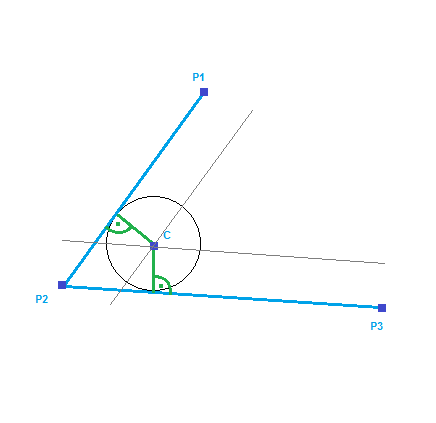
1. displace your lines P1P2 and P2P3 by radius r inwards

   So you need a normal vector of the plane P1P2P3 for example:

   n = normalize(cross(P2-P1,P3-P1))
   

   now just create displacement vectors (polarity depends on your winding rule)

   d12 =  /- r*normalize(cross(P2-P1,n))
   d23 =  /- r*normalize(cross(P3-P2,n))
   

   and displace

   A12 = P1   d12
   B12 = P2   d12
   A23 = P2   d23
   B23 = P3   d23
   

2. compute intersection of displaced lines A12B12 and A23B23

   This will give you the circle center C of your arc. Here is line line intersection computation taken from my C geometry engine:

    line3D closest(line3D l0,line3D l1)
        {
        vec3 u=l0.p1-l0.p0;
        vec3 v=l1.p1-l1.p0;
        vec3 w=l0.p0-l1.p0;
        float a=dot(u,u);       // always >= 0
        float b=dot(u,v);
        float c=dot(v,v);       // always >= 0
        float d=dot(u,w);
        float e=dot(v,w);
        float D=a*c-b*b;        // always >= 0
        float t0,t1;
        point3D p;
        line3D r,rr;
        int f;                  // check distance perpendicular to: 1: l0, 2: l1
        f=0; r.l=-1.0;
        // compute the line3D parameters of the two closest points
        if (D<acc_dot) f=3;    // the lines are almost parallel
        else{
            t0=(b*e-c*d)/D;
            t1=(a*e-b*d)/D;
            if (t0<0.0){ f|=1; t0=0.0; }
            if (t0>1.0){ f|=1; t0=1.0; }
            if (t1<0.0){ f|=2; t1=0.0; }
            if (t1>1.0){ f|=2; t1=1.0; }
            r=line3D(l0.p0 (l0.dp*t0),l1.p0 (l1.dp*t1));
            }
        // check perpendicular distance from each endpoint marked in f
        if (int(f&1))
            {
            t0=0.0;
            t1=divide(dot(l0.p0-l1.p0,l1.dp),l1.l*l1.l);
            if (t1<0.0) t1=0.0;
            if (t1>1.0) t1=1.0;
            rr=line3D(l0.p0 (l0.dp*t0),l1.p0 (l1.dp*t1));
            if ((r.l<0.0)||(r.l>rr.l)) r=rr;
            t0=1.0;
            t1=divide(dot(l0.p1-l1.p0,l1.dp),l1.l*l1.l);
            if (t1<0.0) t1=0.0;
            if (t1>1.0) t1=1.0;
            rr=line3D(l0.p0 (l0.dp*t0),l1.p0 (l1.dp*t1));
            if ((r.l<0.0)||(r.l>rr.l)) r=rr;
            }
        if (int(f&2))
            {
            t1=0.0;
            t0=divide(dot(l1.p0-l0.p0,l0.dp),l0.l*l0.l);
            if (t0<0.0) t0=0.0;
            if (t0>1.0) t0=1.0;
            rr=line3D(l0.p0 (l0.dp*t0),l1.p0 (l1.dp*t1));
            if ((r.l<0.0)||(r.l>rr.l)) r=rr;
            t1=1.0;
            t0=divide(dot(l1.p1-l0.p0,l0.dp),l0.l*l0.l);
            if (t0<0.0) t0=0.0;
            if (t0>1.0) t0=1.0;
            rr=line3D(l0.p0 (l0.dp*t0),l1.p0 (l1.dp*t1));
            if ((r.l<0.0)||(r.l>rr.l)) r=rr;
            }
        return r;
        }
   

   Each line has endpoints p0,p1 and displacement/direction dp=p1-p0 and length l=|dp|. The function returns 2 closest points to each other one belonging to line l0 and the other to l1 so if they match (their distance is near zero or less) they are the intersection C we are looking for. If not the lines are either parallel or too short or far from each other (or you chose wrong polarity for one or both displacements)

3. compute arc endpoints

   Pa = C - d12
   Pb = C - d23
   

4. compute basis vectors u,v for your arc

   for exmaple:

   u = Pa - c
   v = cross(u,n)
   

5. compute edge angles for you arc

   As I chose u as start of the arc directly we need just the ending angle

   d = -d23/(r*r)
   ang = atan2(dot(d,v),dot(d,u))
   // if (ang>M_PI) ang-=2.0*M_PI    // use smaller arc however usual atan2 is in <-PI, PI> range so no need for this
   

6. render your arc

   any point on your arc will be computed like this:

   p(a) = C   u*cos(a)   v*sin(a)
   a = <0 , ang>
   

In case you are not familiar with 3D vector math operations (dot,cross,..) you can find their equations and implementation in here (look for [Edit2]):

• Understanding 4x4 homogenous transform matrices